全く関係ない分野の人物であるハインリヒ＝ヘルツが、コンタクトメカニクスを開拓したことは驚くこと事ではないでしょうか。一目見て、二つの弾性体が自然に接触をしている状態が、電磁気学とは全く関係ないとわかります。しかし、ヘルツ氏はコンタクトメカニクスが電磁気学に対して数学的な類似性を持つと考え、その分野の研究に取り組みました。彼の功績は小さいながらも過去百年の間後世に忠実に受け継がれました。
1877年、ヘルツ氏は二十歳のときエンジニアになることを志し、ミュンヘンへの留学をしました。しかし、彼が留学先に到着すると自分の想像が疑念に支配され始めました。それでも、「エンジニアになるのには実用的だと思える理由がたくさんある。」「まだ自分は失敗した実感と己に対する失望しか感じていない」と、両親への手紙に記しました。ヘルツ氏は地元のハンブルグで勉強している時期に自然科学に興味を持ち、他にも測量学，建築構造学，建築材料学，それに類似する工学にも魅せられ、これらが自分の生涯を費やすのに値すると考えるようになりました。そのなかでもヘルツ氏は数学，メカニクス，そして物理学にさらに深く興味を持つようになりました。彼は両親の助言に従って、物理学コースを選択しミュンヘンに留学して一年後、編入先ベルリンでヘルマン＝フォン＝ヘルムホルツ，グスタフ＝キルヒホッフの両名に師事しました。
1878年10月、キルヒホッフ師の講義を受け始めていた時期にヘルツ氏は掲示板で賞金付の電磁気学に関する問題を見つけました。ヘルツ氏はヘルムホルツ師にこの問題を研究する許可を要望したところ、問題を解くための実験室を割り当てられました。ヘルツ氏の手紙には「毎朝興味深い講義を聴き、忙しい時間を過ごしてから4時までに研究室へ向かう。その後、図書館か割り当てられた部屋で問題の研究に取り掛かった。」と、記されています。そして、彼は問題に対し「電流の運動エネルギーが数値の上限を決定する」と結論付け賞金を得ました。
次に、ヘルツ氏は博士テーマである「動く伝導体の作る電場の分布」の研究に取り組みました。この研究はヘルムホルツ師に深い印象を与えたので、「マグナ＝カム＝ローデ」に加え「アキューミニス＝エ＝ドクトリン＝スペシメン＝ローダビル」を受賞しました。1880年、ヘルツ氏はヘルムホルツ師の今で言うところの助手になり、三年間は「ポスト＝ドクター」の立場で経験を積むようヘルムホルツから言われました。
ヘルムホルツの助手になりヘルツはすぐに、当時ベルリンでかなりの議論の対象であった
ニュートンリング現象に関心を持つようになった。2つのレンズが接触して置かれたときの光学現象に関しては知られていたが、接触面でのレンズの変形に関してそれほど知られていたわけではないとHertzは思った。ヘルツは特に接触している2つの表面間の局所化された変形の性質と圧力分布に関心を持った。彼は、ここで繰り返す価値のある特定の境界条件を満たした接触の表面に形を割り当てようとした。
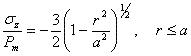
この圧力分布は、接触面の中心で(平均接触圧力の1.5倍となる)最大値に達する。また、（ｒ＝aの地点である）接触面の端では0まで値が下がる。ヘルツは内側のあらゆる箇所の応力の規模は計算しなかったが、計算した表面応力値と左右対称軸に沿った応力値の間を補完することで、応力の特徴についての考えを述べた。1904年にフーバーが最初に完全接触時の応力領域を詳細に計算したようであり、後にフックが1913年、モレトンとクロースが1922年に計算している。最近になって、圧子幾何学の多様性に一致するスネッドンの積分変換法が、軸対称な垂直応力分布に利用されている。脆性固体において、最も重要な応力は垂直応力ではなく、試料表面における接触面の端で最大値になる、半径方向の引張応力である。これは、自分の車のフロントガラスに石が衝突した経験のある人には知られた、「円錐割れ」の構成要因である応力である。この「割れ」は、「ヘルツの円錐割れ」と呼ばれている。
ヘルツは「弾性体の接触について」というテーマに基づいた研究を発表した。しかし、そのことによって、彼は技術者たちの間から悪評を得てしまった。この技術者たちの悪評によって、ヘルツは硬さの重要性の更なる調査へと身を投じ、「科学者は街にいる人達のような曖昧な考えしか持っていない」という考えに至った。とても早い時期から、硬さは浸透や永久変形に対する抵抗を示すと理解されている。スクラッチ法のような便利で簡単なものもあるが、初期の硬さ測定の方法はあまりに多くの変数を必要としたので、硬さの科学的な定義については意味がなかった。ヘルツは、硬さの絶対値は接触領域の中心の永久ひずみを生むために必要な球状圧子直下の最小値であると仮定した。ヘルツの提言によって具体化された硬さ測定は、1900年のブリネル試験や1904年のショアスクルロスコープ、1920年のロックウェル試験、1924年のビッカース硬さ試験、そして1934年のヌープ硬さ試験のような試験の基礎を形作った。
この重要な実質上の問題である硬さについて研究するのに加え、ヘルツは大気中の蒸発と湿度についての調査も始めた。ヘルツは両親にあてた長い手紙の中で、彼の理論と実験について述べた後、次の言葉で締めくくった。「この手紙の内容はとても長くなってしまい、その郵便料で私は破産してしまう。しかし、親愛なる両親、兄弟、姉妹を乾燥させるわけにはいかない。」
ヘルツは電気実験や高電圧放電に多くの時間を費やしたが、彼は依然として様々な問題、例えば氷が水に浮くといった現象に興味を持ち続けていた。ある円板を水に浮かべようとすると沈んでしまうが、おもりを円板上に置くと円板が水に浮くことをヘルツは観察した。この逆説的な結果は、おもりが円板を曲げ、ボート状の形に変えたことにより、円板とおもりが水に浮くと説明できる。ヘルツは「浮遊している弾性板の力学的平衡状態」という論文を発表した後、マクスウェルの電磁気学の研究にほとんどの時間を費やすようになったが、その研究は流体力学とは異なる分野の研究だった。
ヘルツが２０代の時に残した功績は、今日の技術者達の閃きの元となっている。今では、数学や計算技術の発展によって、我々は弾性、または弾塑性接触におけるくぼみの応力場の詳細を描くことができる。ヘルツの功績がなければ、硬さの科学は曖昧なままであっただろう。硬さは材料の特性なのだろうか。ヘルツはそのように考え、他の多くの研究者も同様に考えている。しかし、多くの研究者は硬さが測定方法に依存していると認めており、この分野は依然として科学的調査が求められている。
読者が力や変位のような共通の工学用語について知っているが当然だと思うが、応力、ひずみ、弾性係数、ポアソン比、その他材料特性という工学用語を知っているとは限らない。これらの２つの章の目標は読者にこれらの基本原理に通知して、教育して、そして、個体間のくぼみおよび接触について、後の章のための基礎を準備することである。
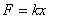（1.2.1a）