英文輪読 第2回 5月1日
(野澤 訳)
1.2.2 フックの法則
図1.2.1によれば、1つの原子が他の原子から、外部の力によって、ゆっくり引き離されていることが分かる。その原子間の化学結合を壊すために必要な外部からの力の最大値は凝集力と呼ばれている。この凝集力を壊すために、少なくともこの図に示す量の力が使われなくてはならない。一度結合を壊して離していくと、原子同士が離れて存在し、それを留めておくのに必要な力が小さくて済むので、どんどん必要な力が小さくなる。定義によれば、結合の力は凝集力の最大値に等しい。
一般に、変位‐力曲線の形は図1.2.1に示すように、一部のサイン波によって近似される。その影響のある領域は、平衡な地点から最大力を示す地点までの部分である。この領域において、
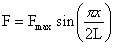
(1.2.2a)
Lは平衡地点からFmaxまでの距離である。今、θが微小なのでsinθをθと近似してみると、変位xが小さい時に必要な力Fは次のようになる。
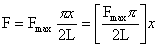
(1.2.2b)
今、LとFmaxは特定の物体については一定とみなす。さらに1.2.2b式に、フックの法則として有名なF=kxを代入する。この結果は、単位面積当たりの分散された力に簡単に展開できるため、
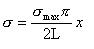
(1.2.2c)
σmaxは物体の引張強さであり、圧力単位である。
もしL0が平衡地点の距離ならば、変位xを使ってひずみεは次のように定義される。
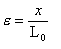
(1.2.2d)
それゆえ、
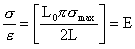
(1.2.2e)
(Aiman 訳)
角括弧のすべての用語は、どんな特定の材料でも一定であると考えるかもしれない(平行位置の周りの微小変位において)。したがって、材料の単一特性Eは弾性係数率またはヤング率で表すことができる。方程式1.2.2.eは、フック法則のよく知られている形式で、それは、言い表すと応力はひずみと比例することである。
実際にやってみると、どんな材料も「理論上」の引張強さほど強くない。通常、弱点は結晶面の横切った滑り、不純物および機械的欠陥によって生じる。応力が適用される場合、通常はこの弱点で割れが始まり、故障が理論上の引張強さ以下によく生じる。工学便覧の実際の引張強さの値は標準試験片の実験結果から得られる。実験で見られるように、幾何学的形状と材料の状態に関する補足知識は与えられた応力で割れが特定の試験片に起こるかどうかによって決まる。
1.2.3 ひずみエネルギー
一次元では、作用している力Fは平衡位置からの原子の微小変位dxを引き起こし、ポテンシャルエネルギーにおいてdWの変化が生じる。総ポテンシャルエネルギーはフック法則から以下の方法で決定できる。
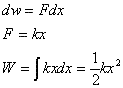
(1.2.3a)
このポテンシャルエネルギーWは「ひずみエネルギー」と呼ばれている。材料を応力があるところに置くことは、外部エネルギー源から材料内部のひずみポテンシャルエネルギーへの伝達を含んでいる。応力が取り除かれるなら、ひずみエネルギーは解放される。解放されたひずみエネルギーは運動エネルギー、音、光、あるいは下に示されているように材料内の新しい表面の形成に変換されるかもしれない。
(塚田 訳)
応力が結合を壊すまで上昇すると、ひずみエネルギーは結合ポテンシャルエネルギーとしてみなすことができる。2つに分けられた原子は、他の原子と結合するポテンシャルエネルギーを持っている。今、互いに分けられた原子は「表面」とみなすことができる。したがって、固体を構成する多くの原子のうち、表面の原子は内部に比べて高いエネルギー状態である。この種類のエネルギーは量子物理学の用語でのみ説明することができる。このエネルギーは材料の「表面エネルギー」と同等である。
1.2.4 表面エネルギー
図1.2.2.に示すように、固体または液体中の深い位置にある原子を「A」とみなす。原子Aには全方位において長距離における化学的引力と、短距離におけるクーロン斥力が等しく働き、材料中で平衡位置を取っている。今、表面上の原子を「B」とみなす。原子Bは表面直下の多くの原子と、さらに奥の原子によって引き寄せられる。なぜなら、原子間に働く引力は「長距離」だからであり、その力の働く範囲は原子寸法を大きく上回っている。しかし、対する斥力は表面直下の少数の原子によってのみ与えられる。なぜなら、斥力は「短距離」だからであり、その力は原子直径のオーダーの範囲内までしか作用しない。表面原子の力の釣り合いについて考えると、表面直下の原子による反発力は、標準的に生じる力よりも増加しているはずである。この増加は表面原子の内部への移動によるものであり、表面直下の原子により近くなる。表面原子が直下の原子に近づくほど、斥力は大きくなる(図1.2.1参照)。したがって、表面原子は表面直下の原子による斥力と、表面直下および内部の原子による引力が釣り合う位置まで内部に移動する。
(高木 訳)
固体または液体の表面は材料本体に収縮包装されている薄い張力の皮膜のようにふるまう。
液体において、この影響は表面張力現象としてよく知られており、これは原子の
表面境界層のポテンシャルエネルギーによるものである。固体の表面にもポテンシャルエネルギー
があるが、固体は液体ほど簡単に変形しないので表面張力の影響は容易に観察できない。
材料の表面エネルギーは、表面が原子のように他の原子との化学結合を作るために持っている
ポテンシャルを意味する。表面のポテンシャルエネルギーは、表面の原子とそれらの表面直下との
結合内部の圧縮ひずみエネルギーの増加として保存される。この圧縮ひずみエネルギーは、
表面下から受ける長距離引力に釣り合うために必要な短距離斥力のわずかな増加により起こる。
1.2.5 応力
工学文脈における応力は力をその力が作用している表面積で割られて得られた数を意味する。
引張と圧縮は共に垂直応力であり、力が考慮中の平面に対して垂直の時起こる。
対照的に、平面に沿ってまたは平行の時せん断応力は起こる。
異なる型の応力の区別を容易にするために、記号σは垂直応力、記号τはせん断応力とする。
材料中の任意な点での応力の合計は垂直とせん断の両応力に関して与えなければならない。
(保苅 訳)
応力の概念を図示するのに、図1.2.3(a)で表されるx,y,zの三軸による立方体で考える。力は面に垂直な成分であるx方向,y方向,z方向にそれぞれ対応したdFx ,dFy,dFzの三成分で構成されている。応力の定義は作用面で分類され、演算子iとjを使うことで私達は応力の構成を説明できる。また、演算子iは作用面に対し直行、演算子jは応力の作用する方向と定義されている。dFx成分は作用面に垂直に作用し、応力は垂直応力、つまり引張・圧縮応力で表す。
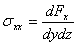
(1.2.5a)
記号σxxは添え字の情報からx方向に垂直な平面に加わる垂直応力を表し、図1.2.4.の通りになる。一般的に、引張応力は正・圧縮応力は負で定義されている。記号による値の割り当ては完全に独断的であり、例えば岩石力学の文意内では、圧縮応力は観測方法の失敗に大きく支配されてるため、便利なことに、この時の圧縮応力は正の値として扱われている。力成分dFyは面と直行しているが、平面に働く力線はτxyで示されるせん断応力ほどである。また、最初の添え字xは作用面がx軸に垂直であること、次の添え字yは応力の作用方向を表す。
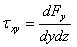
(1.2.5b)
力成分dFzによる平面に作用する垂直応力も同じように表す。
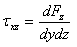
(1.2.5c)