英文輪読 第3回 5月8日
(高木 訳)
せん断応力は方向も割り当てられる。また割り当ては全く任意であるが、それは通常応力を生じている力の作用線の方向と物体の外部表面への垂直方向の応力の符号が同じ時、正のせん断応力が起こる。それ故、せん断応力τxyとτxzは図1.2.4の正で示される。同様に平面dxdzと平面dxdyに作用している力の成分について考えると微小要素dxdydzに対する応力の合計9つの式が導かれる。それを行列表記すると以下のように表せる。
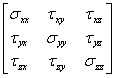
(1.2.5d)
この行列の対角成分σijは垂直応力である。せん断応力はτijによって与えられる。もし力の微小要素の平衡状態を考慮するなら、τxy=τyx、τyz=τzy、τzx=τxzのように行列方程式1 2 5 dは対称形でなければならないことがわかる。垂直応力に関してσxxをσxのように第2の添え字を省略することは便利である。方程式中の応力マトリクスの9つの成分である1.2.5dは応力テンソルと呼ばれる。スカラー場(例えば温度)は単一値x、y、zの関数によって表せる。
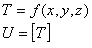
(1.2.5e)
ベクトル場(例えば電界)は3つの成分、Ex、Ey、Ezによって表せる。これらの成分の各々はx、y、zの関数である。
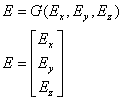
(1.2.5f)
ここで、
(塚田 訳)
応力テンソルのようなテンソル場は9個の成分からなり、式1.2.5dにあるようにそれぞれx、y、zの関数である。応力テンソルは材料のせん断を支える性質によって生じている。材料に力を加えると大抵、垂直応力(引張応力、圧縮応力)とせん断応力の両方が発生する。せん断を支えることのできない材料(非粘性流体など)において、応力テンソルは対角行列になる。非粘性流体において、垂直応力の成分は等しくなり、その結果、圧力が全方向に等しく分布する。
応力を平均応力と偏差応力の和として考えると扱いやすくなる。
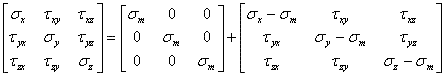
(1.2.5g)
平均応力を次のように定義する。
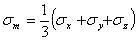
(1.2.5h)
ここで、σx= σxxとし、他も同様とする。残る応力、偏差応力成分は平均応力と共に、材料内の実際の応力状態を表している。平均応力は試験片の体積変化(膨張)に関係し、偏差応力は形状の変化に関係している。図1.2.3bの軸対象系についても同様に考える。
図1.2.5に示すように、x軸と角度θをなす平面daに働く応力を考える。ただし、平面daの法線はz軸に垂直である。
平面daに働く垂直応力は次のようになる。
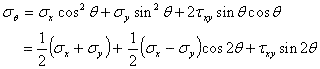
(1.2.5i)
そして、せん断応力は次のようになる。
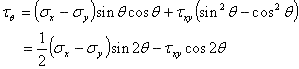
(1.2.5j)
(保苅 訳)
数式1.2.5iより、θ=0の時σθ=σxが成立することが予想される。なお、θ=π/2の時σθ=σyである。θが0から360°の間で、応力σθとτθもまた変化し、最小値と最大値が成立する。この点で、τθ=0になる角度θを決定することに関心が向く。数式1.2.5jより次の式が展開される。
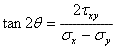
(1.2.5k)
この式より、σθが最大値のときにτθ=0が成立する。
また、この式は章1.2.10で詳しく説明される。
1.2.6 ひずみ
1.2.6.1 デカルト座標系による表示
ひずみとは応力による作用量を測るために変形との相関を利用した測定指標であり、一般的に数式1.2.2dで表される。x,y,zの三軸で構成されるデカルト座標系で表すと、図1.2.6(a)で見られるように、一連の変位ux, uy, uzと単位伸びもしくはひずみで次のように定義されている。
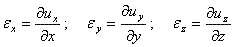
(1.2.6.1a)
垂直ひずみεiは伸展(引張)を正、収縮(圧縮)を負としている。全長がLの一次元要素である丸棒に対し、引張・圧縮により長さがΔLだけ変形した場合について考える。この棒に固定端を基点として長さ方向xに沿って等間隔に点をプロットし変形させると、各区間変位は一様になる。そのため、変位uxと長さxの関係は線形性を持ち、ひずみ(δux/δx)の表示で固定される。このことから、棒の端までの長さであるxがLの時、変位uxが⊿Lとなりひずみ⊿L/Lが導出される。
せん断ひずみは立体要素におけるひずみを表す。図1.2.7(a)にあるように、変位ux,uyと区間P1からP2の間に存在する点Pについて考える。今、変位uyがxと共に立体要素の上辺で線形的に増加する。そのため、垂直応力の定義式uy=εyy及びuy=(δuy/δx)xからy方向における小片の変位が確認され、せん断応力εxy=δuy/δxが定義できる。他の変位も同様に考えられ、x方向のせん断応力で定義される。
(野澤 訳)
しかしながら図1.2.7bの場合を考えると、∂uy/∂xは∂ux/∂yと大きさは等しく向きは反対である。ここで、体積要素は変形ではなく回転しているとする。これは、変形されていない要素において、ひずみポテンシャルエネルギーが存在しているという意味を含むので、εxy=-∂uy/∂x、εyx=∂ux/∂yによって与えられる、せん断ひずみが存在しているということは間違いであるだろう。それゆえ、せん断ひずみを次のように定義するのは、物理的により適切である。
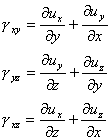
(1.2.6.1b)
せん断ひずみは、体積要素のせん断変形に対して、正しい大きさを持っているが、純回転について0まで減少するのは明らかである。
多くの技術者用のテキストは、せん断ひずみの定義の基準として変形角を使用するのを好んでいる。図1.2.7aの角θを考えてみる。変形後、初めに90度であった角θは∂uy/∂x+∂ux/∂yに等しくなる要素によって減少している。この減少量はせん断角と呼ばれ、σijによって与えられる。
それゆえ、
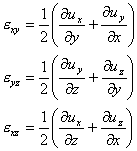
(1.2.6.1c)
εij=1/2・γijであることは明らかである。記号γijは初めは直角だった平面の間の角度の変化として定義された、せん断角を示す。記号εijは応力テンソルせん断ひずみ要素を示し、体積要素の回転の影響を含む。残念なことに、γijという量はしばしばせん断角よりはむしろ、せん断ひずみと称される。それは、弾性方程式において1/2の要素を扱わないことが、しばしば便利であるからだ。そして、この方程式を使えば私たちはとても便利になり得る。