英文輪読 第4回 5月15日
(塚田 訳)
図1.2.7(c)はひずみと回転が同時に起こる場合を表している。体積要素のひずみの程度は図1.2.7(a)と同じであるが、図1.2.7(c)では回転しており、体積要素の底辺がx軸に一致している。ここで、∂uy/∂x=0 であるが、x軸方向の変位はより大きくなっており、以前のせん断ひずみの定義がまだ適用される。図1.2.7(c)の特別な場合では、せん断ひずみの回転成分は変形成分に等しく、単純せん断と呼ばれる。単純せん断という用語は、面に垂直応力を与えず、せん断応力のみを与えた場合に適用される。せん断角は、変形中にせん断角の減少があった場合に正、増加があった場合に負となる。
ひずみテンソルの一般式は次のようになる。
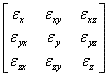
(1.2.6.1d)
そして対称性より、εij=εji であり、他も同様である。また、γij=2εijである。
1.2.6.2 軸対称座標系
多くの接触している応力場は軸対称性を持つため、円柱座標でひずみを考えると便利である。
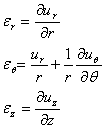
(1.2.6.2a)
そして、せん断ひずみは
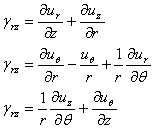
(1.2.6.2b)
ur、uθ、uzは材料内の点のr、θ、z方向の変位であり、それぞれ図1.2.6(b)に示す通りである。また、せん断角γijはせん断ひずみεijの2倍である。軸対称系の問題として、uθはθに独立であり、∂uθ/∂θ=0 である。(また、σr 、σθはθに独立であり、τrθ=0 、γrθ=0 である。)そのため、式1.2.6.2aは次のようになる。
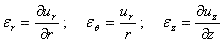
(1.2.6.2c)
式1.2.6.2cは押し込みにおける応力場の応力状態の測定に特に役立つ。その理由は、材料内の変位の点はr、zの関数として計算しやすいからであり(5章参照)、従ってひずみの値を得られ、フックの法則から応力を得られる。
(高木 訳)
1.2.7 ポアソン比
ポアソン比νは、図1.2.8に示すように縦伸びに対する横縮みの比率である。そして、材料が一定容積を維持しようとして、縦応力に対して垂直な横縮みが起こる。ポアソン比νは以下のように与えられる。
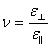
(1.2.7a)
そして、最大値の0.5に近づくとすぐに流体である材料は、一定容積を維持する。すなわち非圧縮性であるのでせん断を支えられなくなる。
1.2.8 線形弾性(一般化フックの法則)
1.2.8.1 デカルト座標系
一般的な場合、応力とひずみは以下のような定数行列Eijklで表せる。
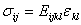
(1.2.8.1a)
等方性の固体(すなわち、あらゆる方向に同じ弾性の特性を持っているもの)について、定数EijklはいわゆるLame定数μ、λの2つまで減少する。2つの材料特性用語でポアソン比ν、およびヤング率Eを言い表すことができる。ここで、
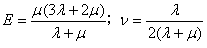
(1.2.8.1b)
「線形弾性」という用語は応力に対する線形依存性を表す変形について言及する。特に延性がある材料で大きな変形をもたらす負荷応力について、応力とひずみとの関係は通常、非線形になる。
1軸の引張または圧縮の状態について、式1.2.2eは応力とひずみの関係を表すのに十分である。しかし、3軸の応力の一般的な状態についてはこの関係を決定する際に横縮みに起こしているひずみを考慮しなければならない。垂直応力とひずみの関係は以下のようになる。
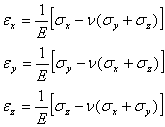
(1.2.8.1c)
せん断応力とひずみの関係は以下のようになる
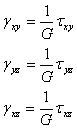
(1.2.8.1d)
ここで、Gはせん断より大きな抵抗を示している高い値、横弾性係数であり、以下のように与えられる。
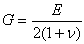
(1.2.8.1e)
また、材料の圧縮性の尺度である体積弾性率Kは
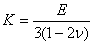
(1.2.8.1f)
(野澤 訳)
1.2.8.2 軸対称座標系
円筒座標系において、フックの法則は次のようになる。
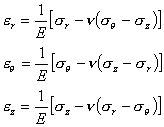
(1.2.8.2a)
1.2.9 2次元平面応力、平面ひずみ
1.2.9.1 応力の状態
固体内の応力の状態は、試験片の次元と応力が支持されている方法に依存する。平面応力と平面ひずみという用語は、一般に2次元荷重系の動作の2つの形態を区別するために使われる。単純に単語の意味では、平面ひずみは大抵厚みのある試験片に適用される。また、平面応力は薄い試験片に使われ、その方向はかかっている荷重方向に対して垂直である。
図1.2.9に示すように、平面ひずみにおいて厚みもしくはZ方向においてのひずみが0ということは、固体の端が位置を固定されていることを示す。つまり、uz=0である。平面応力において、厚さ方向の応力が0ということは、固体の端は自由に動けることを示す。一般に、平面ひずみについての弾性解はν/(1+ν)の代わりに解のνを代入することで、平面応力に変換される。そして、平面応力は、νとν/(1‐ν)を変換することで、平面ひずみと交換される。
1.2.9.2 2次元平面応力
平面応力において、図1.2.9.aのようにσz、τxz、τyzの応力要素は0で、他の応力は厚さ方向( z方向)に通じて分配されている。力は試験片の平面で平行に働いている。そして、z方向の試験片表面では変位は自由である。力が作用している箇所では、固体中の原子は厚さ方向への移動、働いている応力やポアソン比の度合いにより、新しい平衡点を見つけようとする。それ故、
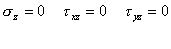
(1.2.9.2a)
となり、我々はフックの法則を使えるので、
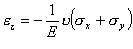
(1.2.9.2b)
(保苅 訳)
1.2.9.3 2次元平面ひずみ
平面ひずみにおいて、図1.2.9(b)より、厚さ方向、または試験片のz方向に沿って加わる荷重は一様である事と、試験片の端ではz方向において変位が抑制され、uz=0になると仮定する。厚さ方向に働く応力σzは次の通りに表せる。
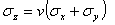
(1.2.9.3a)
このことから、次の式が成立する。
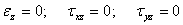
(1.2.9.3b)
応力σzは、厚さ方向もしくはz方向におけるひずみの和が0になる状態を満たした試験片のそれぞれの端に作用する力を上昇させる。εz=0を式1.2.8.1cに代入すると次の数式が求められる。
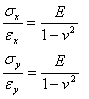
(1.2.9.3c)
係数E/(1-ν2)は効果的な弾性係数と考えられ、弾性係数Eより優れている。試験片の厚さ方向に適用した制限がその剛性を効果的に増加する。
表1.2.1より応力、ひずみ、そして、平面上で作用する応力と平面に作用する応力に対する数式の違いを見ることが出来る。
1.2.10 主応力
固体の各点において、σ1、σ2、σ3の3応力を確認することができ、これらは互いに直角な3平面上で垂直方向に作用し、せん断応力は作用しないものする。応力の作用するこれらの平面の向きが、せん断応力ゼロになる必要条件を満たす固体中の測定点において異なる。そのため、垂直応力のみが平面上に作用し、これらのことを「主平面上の応力」と呼ぶ。主平面上に作用する垂直応力は「主応力」と呼ぶ。ここでは主平面上に作用する応力の中にせん断応力はない。θが0から360°の間で変化するとき、固体中の測定点における作用面の向きで変化する垂直応力は数式1.2.5.iで与えられ、せん断応力では数式1.2.5.jで与えられる。そのため、応力σθとτθは最小値と最大値を持つ。最大・最小垂直応力は主応力のことであり、このときせん断応力はゼロになる。このことは数式1.2.5.kで示された角度で起こる。主応力は固体の任意点で作用する最大垂直応力(つまり引張や圧縮)である。最大せん断応力は主平面に作用する応力と交差する平面上に作用する。主応力は引張・圧縮応力の最大値であることから、それらの数値が固体の機械的強度を研究する上で特に重要である。
(Aiman 訳)
1.2.10.1 デカルト座標系;2次元の平面応力
平面応力の主応力の大きさは、大域座標系のなかでxとyの軸によって、定義された平面に関して作用する応力の点から表すことが出来る。
最大値と最小値 に対して式1.2.5.iでのσθの導関数から得られる。これは
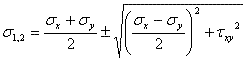
(1.2.10.1a)
τxyはy軸の方向で、x軸に垂直な水面を横切るせん断応力である。τxy=τyxより、その後τyxも式1.2.10.1aの中で使用することができる。σ1とσ2は固体中に肝心の点(x,y)で垂直応力の最高値と最小値である。慣例によって、主応力はσ1>σ2の関係にある。これは非常におおきな圧縮応力(より負数)がその後、非常に小さなσ1>σ2とみなされると注意する。さらなる混乱は岩石力学の分野で発生して、ここで圧縮応力は、便利のため、正の大きさに慣例的に割り当てられる。
主応力は図1.2.10(a)の中で示されるように、x軸への角度θpおよびθp+π/2である平面(つまり主平面)に作用する。応力σ1およびσ2が「垂直」応力であるから、その後角度θp、平面への垂直方向であってさらに応力方向も与える。角度θpは次のものから計算される。
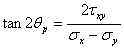
(1.2.10.1b)
この角度は1.2.5の節、式1.2.5.kのゼロせん断の平面に対応することを示している。