英文輪読 第5回 5月22日
(Aiman 訳)
最大値および最小値のせん断応力が、応力の主面の間に適応させられた面を横切って生じる。これらの応力の大きさは等しいが、異符号である。また、便利のため、私たちはそれらを単に最大のせん断応力と呼ぶ。最大のせん断応力はσ1とσ2の間の差の半分である
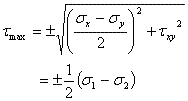
(1.2.10.1c)
プラス記号が最大、およびマイナス記号が最小のせん断応力を表わす。最大のせん断応力の平面の角度θsが大域なx座標軸に関して適応させられて、次の式から得られる。
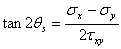
(1.2.10.1d)
この方程式を満たすθsは2つの値がある。θsとθs+90°はτmaxとτminに対応する。角度θsはθpに45°である。
最大のせん断応力の平面に作用する垂直応力は、次の式から与えられる。
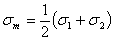
(1.2.10.1e)
私たちはどれを平均応力と呼んでもよい。最大のせん断応力の平面の各々においては、二次元の場合のために、平均応力σmと等しい垂直応力がある。平均応力は軸の選択に依存していない、その結果
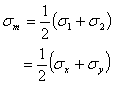
(1.2.10.1f)
1.2.10.2 デカルト座標系::2次元平面応力
平面ひずみの状態のため、xy平面に最大および最小の主応力は、σ1とσ2は式1.2.10.1aに与えられる。平面ひずみの状態は、z方角に本質的な厚さを備えた試験片を指すが、xおよびy方角のみに作用する力によって負荷される。平面ひずみ問題では、ポアソン比に比例した量に対応した厚さ、またはz方向に与えられ、主応力になる。従って、平面ひずみは、
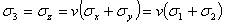
(1.2.10.2a)
慣例では一般にσ1<σ2<σ3であるが、平面ひずみの問題においてσzは大きさに関わらずσ3と同等となる。よって、平面ひずみ状態ではσ3>σ2となることがある。
(高木 訳)
1.2.10.2 軸対象座標系:2次元
応力の点対称は多くの工学問題の中に存在する。そして、関連した弾性解析は極座標(r,θ)に変換することで大いに単純化できる。典型的な極座標系において、半径方向応力σrと接線応力σθが存在する。そして主応力は以下のようになる
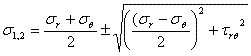
(1.2.10.2a)
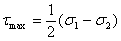
(1.2.10.2b)
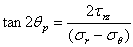
(1.2.10.2c)
せん断応力τrθは軸の左右対称性の場合ゼロになる。従ってσrとσθはこの場合主応力である。
1.2.10.3 デカルト座標系:3次元
上記したように三次元固体において、せん断応力がゼロである3つの直交面が存在する。これらの主平面上の垂直応力σ1、σ2とσ3は、主応力と呼ばれる。固体内の所定の点で、σ1とσ3はそれぞれ垂直応力の最大値と最小値である。そして、σ2の値はσ1とσ2の中間値をとる。3つの主応力は、σの行列式の値を求めることでわかる。
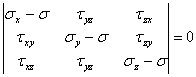
(1.2.10.3a)
方程式1.2.10.3aの解とσの三次方程式、そして得られた3つのσの値は、σ1>σ2>σ3のように、順々に配置される。三次方程式1.2.10.3aの解は実際には少々不便である。そして、主応力σ1、σ2、σ3は式1.2.10.1aで使用しているσx、σy、τxy、とσy、σz、τyzとσx、σz、τxzや、最大値としてσ1、最小値としてσ3を選択して、決めることはより便利である。σ2はそれぞれを組み合わせて計算したσ2の最大値である。
主せん断応力平面は応力の主平面と交わる。これらの平面の各々のせん断応力τの値は以下のように与えられる
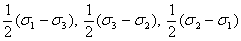
(1.2.10.3a)
(塚田 訳)
以下のことに留意する必要がある。式1.2.10.3aで与えられる応力に名前をつけることはしない。その理由は、どの応力がより大きいか推測的に知ることができないからである。ただし、定義よりσ1<σ2<σ3であるので、最大主せん断応力はσ1とσ3の差の2分の1で与えられる。
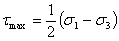
(1.2.10.3b)
最大せん断応力の作用する面の方向は、第1、第2主応力面に対して±45°傾いており、第2主応力面と平行である。
主せん断応力に関わる垂直応力は次の式で与えられる。
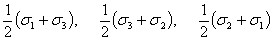
(1.2.10.3c)
平均応力は軸の選択に依存しないので
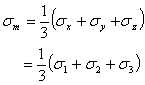
(1.2.10.3d)
ここで言う平均応力は垂直応力ではなく、2次元における主せん断応力面に作用する応力であることに留意する。面に作用する平均応力の主軸の方向余弦l、m、nは等しい。この面に作用するせん断応力は、材料内の塑性流動の基準の公式化に関係している。
1.2.10.4 軸対称座標系:3次元
軸対称は多くの3次元の工学的問題に存在する。そして軸対称に関する弾性解析は、円柱座標(r、θ、z)に変換することで大いに簡易化できる。この場合、半径方向応力σr、軸方向応力σz、周方向応力σθを考えるのは便利である。応力場内に対称性があるため、周方向応力はしばしば主応力となる。σr、σθ、σzはθに独立であり、τrθ=τθz=0となる。くぼみの問題において、次のように主応力の名前をつけると便利である。
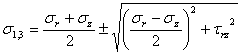
(1.2.10.4a)
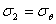
(1.2.10.4b)
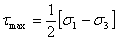
(1.2.10.4c)
図1.2.10(b)はこれらの応力を表している。これらの式を用いると、くぼみ応力場においてときどき σ3>σ2 となる。この場合、今まで通例であったσ1<σ2<σ3の関係に厳密に従わない。主応力のうち、σ1とσ3の2つは、rz面に作用していることに留意する(θは一定)。主応力の方向はr軸に対して次の式で与えられる。
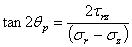
(1.2.10.4d)
(保苅 訳)
数式1.2.10.4dにおいて、正の値θpはr軸から応力の作用線の間で反時計回りに定義されている。しかし、このθpの角度が45°を超えると面倒なことに、θpの定義式はさらに第五章の式5.4.2.oで与えられることになる。主平面と交差する最大せん断応力の作用面は次の式で表される。
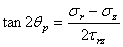
(1.2.10.4e)
1.2.11 平衡方程式と適合条件
1.2.11.1 デカルト座標系の場合
応力の平衡方程式とひずみに関する適合条件は、試験片に対する応力とひずみの変化量の関係で詳細に述べられる。これらの数式は特に応力のみの測定で分析できないシステム(つまり、静的測定システム)における応力とひずみに対する解法に関連性がある。荷重の作用している試験片が平衡であるには、内的応力に対し体積力(例えば、重力もしくは慣性による効果)が作用していないといった特定の状態、次に当てられるNavierの平衡方程式を満たさなければならない。
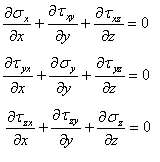
(1.2.11a)
数式1.2.11aは固体内の一点から他点までの応力の変化を詳しく述べている。固体内の各点における変位は、固体内における変位の変化を規定する状態で適合条件があることを満たすことが要求され、次の式で与えられる。
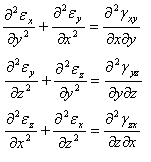
(1.2.11b)
互換関係は物体内の変位が試験片に対して円滑に変化することを示唆する。一般的な弾性体の問題を解く方法は、問題に適合した境界状態であることを前提として、平衡と適合条件を両立させた各応力成分に対する数式を要求する。これらの条件を満足する本質的な公的の解法は1862年、Airyによって実証された。
(野澤 訳)
1.2.11.2 軸対称座標系
似たような考えは、体積力を無視した円筒極座標系における、軸対称応力系に使われる。
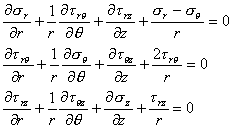
(1.2.11c)
τrθと はZ軸周りの対称に関して0まで減少する。
1.2.12 サン・ブナンの原理
サン・ブナンの原理は工学的構造物における応力の分析に役立つ。その原理では、合力とモーメントが変わらなければ、つまり静的に同等な力ならば、応力やひずみや力の作用とは全く異なった試験片中の弾性変位は変化せず、実際の負荷の形式には無関係である。例えば、接触の問題において、圧子直下の局所的変形は圧子の形状に依存するが、広い範囲の応力分布はおそらく、圧子の形状に依存しない。
1.2.13 静水圧応力と偏差応力
与えられた物体の体積要素について、その要素において働くσx、σy、σz、τxz、τyz、τzxという応力は、平均成分や偏差成分を導くのに便利である。平均応力は次のように決まる。
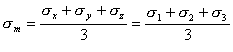
(1.2.13a)