英文輪読 第6回 5月29日
(Aiman 訳)
残留応力の成分は、要素のひずみに対して関連がある応力の実際状態を発生するときに必要となる。偏差な応力、あるいは偏差応力として知られている。
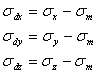
(1.2.13b)
塑性流動(すなわち降伏)が一般に、一定の静水圧応力の適用ではなく試験片のひずみの結果生じるので、応力の偏差成分は特別に興味がある。応力偏差は軸選択に依存している。静水圧成分は依存してない。従って、主偏差応力は次のとおりである
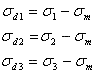
(1.2.13c)
偏差応力の極大差は、方程式1.2 .10.4cの中で定義された最大のせん断応力と直接関係のあることを容易に示されるσd3を引いたσd1から与えられる。
偏差応力の成分に関連した次の特性に気をつけた方が便利である。
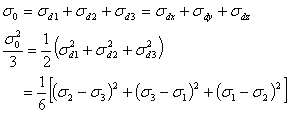
(1.2.13d)
σ0は一定と見なされていて、この式は降伏条件として使われている材料の降伏応力に直接関係がある。8面体面に作用するせん断応力は「8面体」せん断応力と呼ばれている。
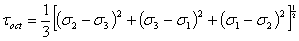
(1.2.13e)
(塚田 訳)
1.2.14 応力の視覚化
ひとつの図表において、材料中の点の完全な応力状態を表示することは難しい。応力の様々な特性を個々の図表で表示することは、より便利である。等応力線(等圧線)は一定応力の曲線である。垂直応力、せん断応力は大域的、局所的、または主座標軸に対して説明される。応力の方向は、等応力線上にある点の接線に対する法線では与えられない。等応力線は、応力の方向に関する情報を与えない。等応力線は、応力の大きさの情報のみを与える。
応力曲線は曲線であり、その接線は接触点における応力の一点の方向を表す。そして応力曲線は、応力の働く方向の視覚化に特に役立つ。主応力を応力曲線で描くとき、それぞれの主応力の曲線は直交する。応力曲線上の点の接線は、応力の作用線を表す。応力曲線は応力の大きさについての情報を全く与えない。
いくつかの特別な応力状態は、実験観察に比べて簡単にするために、一般的に図で示される。例えば、光弾性法により求めた等応力線は、せん断応力の等応力線と同等であると見なされる。延性の試験片に起こる滑り線は、せん断応力曲線と同等であると見なされる。
1.3 塑性
多くの接触荷重状態において、試験片材料の弾性限界は突破され、不可逆な変形になる。完全な塑性状態において材料は、応力が作用すると一定のひずみを示す。それゆえ、ひずみの総計は応力の作用している時間の長さに依存している。よって、塑性を理論的に扱うことは、ひずみの時間変化率を含んでいる。これを「塑性流動」と呼ぶ。
(高木 訳)
1.3.1 塑性流動式
粘性は流れの抵抗であり、その粘性係数ηは以下のように与えられる。
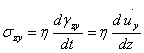
(1.3.1a)
一定流量の場合の流量の式はナビエ・ストークス式として知られている。
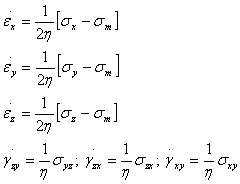
(1.3.1b)
ここで、せん断ひずみの変化率γxyは次のように与えられる。
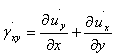
(1.3.1c)
yzやzxの場合も同じである。
式1.3.1b塑性流動が起こらず、特に興味深い応力の偏差成分であることを示している静水圧応力の状態のためにゼロに減少する。それ故、式1.3.1bはこのように書ける。
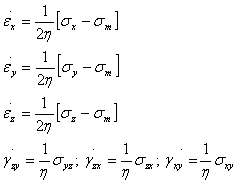
(1.3.1d)
ここでσmは平均応力である。
塑性はせん断応力または偏差応力にとても依存しているので、「すべり線」として塑性領域の応力場で表すのは便利である。すべり線はすべての点においてせん断ひずみの最大率の方向の曲線である。最大せん断応力は3つの主平面のうちの2つに交わる平面に沿って起こるので、各々の点において2つの最大せん断ひずみの方向を持っている。
(保苅 訳)
1.4 応力の破損条件
前章において、塑性体である材料の機械的性質を決定する数式を要約した。
見たところでは、材料の示す弾性もしくは塑性状態に基づいて測定できることが相当に興味深い。
多くの場合において、塑性流動は荷重の作用している試験片の破損した状態とみなされている。
それぞれの破損基準は塑性変形の発現を予測しようと試みている存在であり、偏差の応力状態を静水圧の応力状態より気に懸けることは、塑性体の性質を前者で定義したため驚くべきことではない。
1.4.1 トレスカの破損条件
せん断応力は塑性降伏において、一般的にトレスカが提唱した「最大せん断応力が材料に対し降伏応力(引張もしくは圧縮で測定された)の半分の値に達した時、塑性変形が発生する」という事柄から重要な役割を担っている。
ある単純な例において、一様な引張が作用している場合では、(最大主応力)σ1は作用している引張と同等であり(最小主応力)σ2=σ3=0が成立する。
降伏は応力σ1が物体に試験をして得た降伏応力Yに達した時発生する。
さらに、塑性流動に対するトレスカ条件は次の式で表せる。
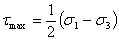
(1.4.1a)
もしくは、次のように簡略化して表す。
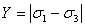
(1.4.1b)
これらの式におけるσ1とσ3は最大・最小主応力である。
二次元の平面応力と平面ひずみに対しては、最大せん断応力の解釈と定義について注意を要する。
通常、厚さ方向の応力はこれらの問題においてσ3と表示され、平面応力σ3=0,平面ひずみν(σ1+σ2)と表される。
平面ひずみについては、最大せん断応力の作用面は通常z軸、もしくは厚さ方向に平行である。
平面応力については、最大せん断応力は通常z軸もしくは厚さ方向と45°傾いた平面上で発生する。
(野澤 訳)
1.4.2 ミーゼスの破損条件
静水圧的というよりはむしろ、応力の偏差要素は塑性流動や降伏による試験片の破壊に関係することが分かっている。3次元の場合、応力の偏差要素は次のように表記される。
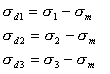
(1.4.2a)
降伏条件は、どの軸かを選択することには依存しないことが望ましく、それゆえ我々は塑性流動に役立つ条件を明確にするために、式1.2.13dによって与えられる偏差応力の不変性を使う。ミーゼスの降伏条件によると、次のようになる。
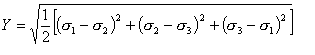
(1.4.2b)
Yは引張・圧縮における、物質の降伏応力である。式1.4.2.bは物質のひずみにおける、ひずみエネルギーに関係があることを示しており、また、この式は式1.2.13.cによって定義された八面体応力の説明にもなっている。この条件では、ひずみ時のひずみエネルギー、もしくは八面体せん断応力が物体の特性値と等しくなる時に、降伏は起こるとしている。
εz=0という平面応力の特別な場合について、XY平面の応力と変位はZの値に独立である。Z軸は主平面に一致し、σz=σ2である。これによって、ν=0.5である非圧縮性の物質について、σ3=1/2(σ1+σ2)が成立する。それゆえ、式1.4.2.bから次のようになる。
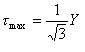
(1.4.2c)
τmaxは式1.2.10.3.bによって与えられる。
任意の2つの主応力も等しいという特別な場合、トレスカとミーゼスの条件は同じである。条件の選択は、より一般的に光学を扱う者達に使われる。それは多くの物質・負荷システムについての実験観察により、一致しているようであるからだ。