英文輪読 第7回 6月5日
(野澤 訳)
上記で考慮された2つの破損条件は、物質中のせん断応力に関係する塑性変形の始まりに対応する。脆性物質について破損は大抵亀裂の成長によって起こり、唯一特別場合において塑性変形が起きる。しかしながら、後の章で示すように、脆性物質の塑性変形は、いつも決まって塑性変形を促進させる応力の状態を必要とする、押し込み応力場を調べる硬さ試験において起こる。
2章 線形弾性破壊力学
2.1 はじめに
石器時代の斧の製作から始まり、様々な物質の強さ(外見、コスト、有用性や神から授かった財産と同じくらい重要な)についての直感と経験は、多くの工学的構造物の設計の基礎として役に立った。19世紀の産業革命によって、技術者は石や木のような伝統的な材質の代わりに、鉄や鋼を使うようになった。石とは異なって、鉄や鋼は引張りに強いという長所を持っていて、それゆえ、工学的構造物は以前より軽く、安く済むようになった。第二次世界大戦直前のころ、技術者は、単純はり理論を使って計算するように、最大応力は物質の引張強さのある割合のところまで制限されるということを確信していた。様々な物体の引張強さは、研究室において簡単に測定することができ、様々な物質の結果は標準的な参考書に用いられていた。しかし、残念なことに、この基礎に基づく構造物の設計は結果として、多くの失敗に繋がっている。なぜなら、特定の構造物の強さにおいて、物体の端や穴の所で、応力が上昇する効果が技術者に認識されていなかったからだ。この失敗により、破壊力学の分野が発生したのである。破壊力学は物体の破壊に対する抵抗の特性を示そうとしている。つまり、靭性である。
(Aiman 訳)
2.2応力集中
靭性の量的定義への前進は1913年にイングリスの仕事から始まった。
イングリスは、応力平板の角か穴のまわりの局部応力が平均負荷応力より
何倍も高いことを示した。鋭角、切り込みあるいは亀裂の存在は、これらの部分に負荷応力を集結させる役目をする。イングリスは弾性理論を使用して、応力平板の穴の端にある拡大の応力度は穴の曲率半径によって依存することを示した。
曲率半径が小さいほど、応力集中は大きい。イングリスは、「応力集中係数」κが楕円の穴において次のものと等しいことを知った。
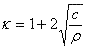
(2.2a)
ここでcは、穴の半径でρは穴の先端の曲率半径である。
非常に狭い楕円については、応力集中係数は非常に1以上かもしれない。丸穴において、方程式2. 2aはκ=3である(図2.2.1に示されたように)。応力集中係数は穴の実寸や長さに依存してないが、曲率半径に対するサイズの比率だけに依存することが注目されるべきである。
(塚田 訳)
2.3 エネルギー平衡方程式
1920年、イングランドの王立航空機関に所属するアラン・A・グリフィスは、交番加重を受ける機械部品の力による引掻きの効果と表面仕上げについて興味を持った。イングリスの理論で、亀裂または割れの先端における応力の増加は、亀裂の幾何学的形状にのみ依存し、亀裂の大きさには依存しないとあるが、これはよく知られる事実とは正反対である。大きい亀裂は小さい亀裂に比べてより容易に広がる。この例外がきっかけで、Griffithは最小ポテンシャルエネルギーの観点に基づいた破壊の理論的解析をするようになった。グリフィスは、亀裂の形成によるひずみエネルギーの減少が新しい割れ面に必要な表面エネルギーに対して等しい、あるいは大きいと提唱した。グリフィスによると、亀裂の成長には2つの条件が必要である。
- 亀裂先端の結合には破損点まで応力が加えられる。亀裂先端の応力は応力集中係数の関数であり、曲率の半径と長さの比に依存す る。
- 亀裂の長さの増加により、ひずみエネルギーは解放されるが、そのエネルギー量は新しい2つの亀裂面に必要な表面エネルギーに 等しいか、より大きい。
2つめの条件を数学的に表すと、次のようになる。
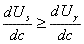
(2.3a)
ここで、Usはひずみエネルギー、Uγは表面エネルギー、dcは亀裂の長さの増加ある。式2.3aは、亀裂が伸びることで、単位亀裂長さあたりのひずみエネルギー放出率が、必要となる表面エネルギーの比率に少なくとも等しいことを表している。グリフィスはイングリスの十分に狭い楕円形亀裂の応力場計算を用いて、解放されるひずみエネルギーを表した。ひずみエネルギーは、長さ2cの両端亀裂で、単位幅に一様な応力σaが与えられている無限板の場合である。
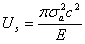
(2.3b)
(保苅 訳)
図2.3.1において、私たちは数式2.3bの半定量的な値を求めることができ、このことはひずみエネルギーが直径2cの円内で解放されたからと考えられる。
そのため、この場合のひずみエネルギーは、U=(1/2σ2c2E)(πc2)で表される。
以上より、綿密に計算された今回のひずみエネルギーをきっかり二倍すると式2.3.bになる。
第一章で述べたように、表面ひずみの場合において、試験片の厚さが重要であり弾性係数EをE/(1-ν2)で表示する必要がある。
この章において、私たちは分母(1-ν2)を省略しているが、適用する式のほとんどにこの分母を含んでいることを注意しなければならない。
図2.3.1に示す亀裂部の2表面における単位幅と長さ2cに関する表面エネルギーの総和は次の式で与えられる。
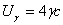
(2.3c)
式2.3cの係数4は亀裂部に長さ2cの断面が二つ存在することから与えられている。
γは固体における亀裂部の表面エネルギーを表す。
コレは一般的に表面自由エネルギーよりも大きく、亀裂の形成が表面から少し深い固体内部に位置する原子を含むためである。
亀裂部の表面エネルギーには他にも散逸機構のエネルギーを含んでおり、微小亀裂,相変態,そして塑性変形などが挙げられる。
そのため、数式2.3b及び2.3cの半径:cに対する導関数を求めるとで、この式により私たちはひずみエネルギー放出率と表面エネルギー創出率を考えられる。
亀裂成長の臨界状態は次の式で表される。
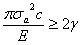
(2.3d)
(高木 訳)
式2.3dの左辺は、亀裂先端当たりのひずみエネルギー放出率で、均一引張負荷応力の働いている無限体の両端亀裂に適用される。式2.3dは亀裂長さ増加当たりのひずみエネルギー放出率が亀裂長さの一次関数であること表しており、また、必要とされる亀裂長さ当たりの表面エネルギー率は一定である。式2.3dは亀裂成長のグリフィスエネルギー平衡方程式である。そして、表面のエネルギー、ひずみエネルギーと亀裂長さの関係は図2.3.2のようになる。
ひずみエネルギー放出率が必要とされる表面エネルギーに達するまで、亀裂は広がらない。この点を超えると、不安定な亀裂成長に至る新しく形成された亀裂面と試験片の亀裂によって必要とされる以上のひずみエネルギー放出が生じ、これによってより多くのエネルギーが利用できるようになる。
図2 3 2に示される平衡状態は不安定であり、試験片の亀裂は平衡状態で起こる。不安定性の存在は、方程式2.3bの二次導関数によって与えられる。d2Us/dc2 < 0時、平衡状態は不安定であり、d2Us/dc2 > 0の時、平衡状態は安定である。図2.3.3は、平衡状態が安定である構成を示している。この場合、亀裂成長は平衡状態で起こるが、亀裂はくさびと同じ比率で材料に広がる。