英文輪読 第9回 6月19日
(野澤 訳)
亀裂先端付近の塑性領域の概念は、多くの技術者や物質科学者によって支持されており、金属の破壊に対して有益な関わり合いを持つ。しかしながら、脆性個体の亀裂先端の存在は、物理学的領域において好ましくないと思われる。式2.4.1aによって予測される応力特異性は、非線形でなく弾性変形によって、脆性体において無効にされる。1章で私たちは、どのように平衡点周りの微小変位に対する、2原子間に線形弾性が働くかを見てきた。亀裂先端では、変位は原子規模では小さくはなく、非線形挙動が予測される。脆性体において、ひずみエネルギーは塑性事象ではなく、転位の動きのような延性金属に起こる原子結合の非線形伸びによって吸収される。故に、脆性材料は無限大の応力が表面のひびや内部の割れの先端で存在するが、最小の負荷がかかる条件下で、バラバラにならない。エネルギー平衡式は、このような拡大するひびについて満たされなくてはならない。
2.4.3 亀裂抵抗
全てのひずみエネルギーが新しい亀裂面の表面エネルギーに利用されるという仮定は、他のエネルギー散逸メカニズムがある延性固体には、適用されない。例えば、結晶性固体において多量のエネルギーが結晶格子の転位の運動に消費される。これは、おそらく材質の極限強度より少ない負荷応力で起きる。延性材料の転位運動は降伏や塑性変形、塑性流動の目安である。アーウィンとオロワンは、グリフィスの式に項を付け加えた塑性領域に関係する、非可逆エネルギーメカニズムを考慮するために、グリフィスの式を修正した。
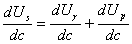
(2.4.3a)
(塚田 訳)
式2.4.3aの右辺は記号Rで与えられ、亀裂抵抗と呼ばれる。グリフィスのエネルギー平衡方程式が満たされる点で、亀裂抵抗は亀裂拡大に必要なエネルギー量の最小値を示し、単位はJ/m2(すなわち、単位幅当たりのJ/m)である。このエネルギーは破壊仕事(単位J/m2)と呼ばれ、じん性の指標である。
延性材料は脆性材料に比べてじん性が高い。その理由は、延性材料が塑性領域においてエネルギーを吸収するためである。そのため、塑性ひずみエネルギーと呼び、これはもはや表面の生成(すなわち亀裂)に利用できない。一方、脆性材料は蓄えられた弾性ひずみエネルギーを、表面生成によって消費することのみが可能である。破壊仕事は実験的に測定することが困難である。
2.4.4 K1C, K1の臨界値
応力拡大係数K1はスケール係数であり、亀裂先端近辺の座標(r,θ)における応力の大きさの特性を示している。異なる2つの試験片の2つの亀裂に、K1がそれぞれの試験片で等しくなるように荷重を与える。その時、それぞれの亀裂付近の応力の大きさは正確に等しくなる。今、負荷応力を増加させ、K1をそれぞれの試験片で一定に保つと、最終的にエネルギー平衡方程式が満たされ、亀裂が伸びる。亀裂先端の応力は正確に等しいが、その値は不明である(理論的には完全弾性体において無限大となる。しかし、実際には弾塑性変形によって制限される)。この亀裂拡大におけるK1の値を臨界値K1Cと呼ぶ。
(保苅 訳)
この時、K1Cを亀裂拡張の始まりであると定義する。
必ずしも試験片の破壊の発生を示唆することは無く、K1Cは亀裂の安定度と関係する。
通常は材料の性質と関連し、じん性を特性付けてから使えるようにすることが出来る。
一方破壊仕事において、その決定は塑性領域内の事象に関する知識との関係は無い。
K1Cの一貫値と再現値は、試験片が平面ひずみにおける試験をした時のみ測定できる。
平面応力において、破壊に対するK1の臨界値は板厚と関連する。
それ故に、K1Cは頻繁に「平面ひずみ破壊じん性」と呼ばれ「MPa m1/2」の単位を持つ。
K1Cの低い値は、応力が与えられて、材料が亀裂の成長する前の短い亀裂長さに抵抗していることを意味する。
K1=K1Cの状態は必ずしも試験片の破壊、もしくは破損と一致するとは限らない。
K1Cは亀裂拡大の始まりを詳細に述べている。
これが安定か不安定かどうかが亀裂系に関係する。
最悪な破壊は平衡状態が不安定な時に発生する。
接触応力により始められる脆性材料の亀裂の場合、亀裂は初めに不安定であり応力領域の鋭い減少によって安定する。
例えば、第七章において、私たちはひずみエネルギー解法率における変化(直接K1に関係する)微分係数dG/dcが初めは正であり亀裂が長くなることで負になることを見る。
応力拡大係数という用語において、亀裂はdK/dc<0で正, dK/dc>0で負である。
K1=K1cの状態にある安定構造は亀裂が拡大の重要な一端であるが、作用応力が増加しない限り広がることは無いことを意味している。
もし、これが起きると、新しい安定平衡亀裂長さが出てくる。
これらの状態下で、各々の亀裂拡大の増分は結果的に解放されるひずみポテンシャルエネルギーが十分であるとみなされる。
不安定形態の場合、亀裂は直に試験片上で急速に拡大し破損を誘発する。
これらの状態では、各々の亀裂拡大の増分において、開放するひずみポテンシャルエネルギーとみなす表面ひずみエネルギーが十分でない。
(高木 訳)
2.4.5 GとKの等価
Gを亀裂先端あたりのひずみエネルギー放出率と定義する。これは式2.3dの左辺によって与えられる。そして、無限固体中の両端亀裂における亀裂あたりのひずみエネルギー放出率は以下のようになる
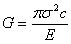
(2.4.5a)
式2.4.1bを式2.4.5aに代入して書き換えると以下のようになる
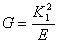
(2.4.5b)
K1=K1C のとき、GCは試験片の亀裂拡張または場合によるが亀裂を引き起こす材料のひずみエネルギー放出率の臨界値になる。K1とGの関係は重要である。なぜなら、それが応力とエネルギー平衡方程式の両方を表すことから、K1C の状態は亀裂成長の必要十分条件であることを意味するからである。
K1C の値は間接的に亀裂先端での応力を表し、さらに亀裂拡張の始まりでのひずみエネルギー放出率でもある。Kのさまざまな補正とそれに関わるGは有次元の量の亀裂であるために必要であることを思い出されなければならない。補正がどうであれ、GとKの関係は式2.4.5bによって与えられる。
式2.4.5bに時々現れるπは、K1で使用している特定の定義に依存する。特に異なる所から式を比較するとき、これらの式の一貫したπの使用は欠かせない。また、式2.4.5bは平面応力状態を表すことを理解していなければならない。実際には平面ひずみの条件はより普通で、その場合には係数1−ν2を分子に含めなければならない。
(Aiman 訳)
2.5 応力拡大係数の決定
2.5.1 応力拡大係数を実験的に測定すること
グリフィスのエネルギー平衡方程式の直接適用は、破壊γの仕事を決定する際の困難さのため、めったに実用的ではない。更に、グリフィス方程式が必要だが、亀裂成長さに対して十分条件ではない。しかしながら、応力拡大係数はより容易に決定され、亀裂成長用の必要十分条件を表わす。しかし、応力拡大係数を決定する際に、形状係数Yが一般に知られていないので、方程式2.4.1bは直接使用することができない。
先に述べたように、Y=2/πは無限板に埋め込まれた半径cの硬貨形成円形亀裂に適用される。一般的なテキストにおいて、このような式が他のタイプの亀裂および荷重の形状についても存在していれば、利用可能である。Kの臨界値を見つけるために、準備した試験片(それは既に導入されていた長さcの亀裂を持っている)に増加する荷重Pを作用させ、いずれかの試験片が破壊した時に、荷重の記録をする。
図2.5.1は、梁試験片が亀裂の存在している側に引張荷重を受けている様子を示している。式2.5.1は、破壊じん性が亀裂長さcと、いずれかの試験片で破壊が起きたときの荷重Pから計算することができる。実際には、周辺効果を避けるために梁試験片の長さが、その高さのおよそ4倍になることに注意する。
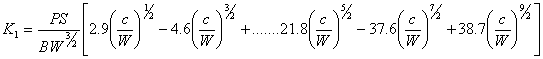
(2.5.1)
破壊じん性の一貫性や再現性のある結果は、平面ひずみの条件でのみ得ることができる。平面応力では、亀裂のKの値は、試験片の厚さに依存する。この理由で、Kの値は、平面ひずみに従って測定されて、用語「平面ひずみ破壊じん性」である。