英文輪読 第10回 7月3日
(高木 訳)
2.5.2 事前の応力から応力拡大係数を計算
ある条件下では、実際に亀裂が存在する前に、固体中の応力場を使っている亀裂経路の応力拡大係数を計算することは可能である。そのやり方は応力拡大係数の重ね合せの特性を利用する。
図2.5.2aに示すように、均一負荷応力σaの働いている無限固体にある内部亀裂長さ2cについて考えてみる。亀裂の存在は亀裂先端付近の応力により増大し、応力拡大係数K1は式2.4.1bから容易に求められる。今、応力と反対方向に一連の表面力を考える。そして、図2.5.2bを示されるように、完全に亀裂を閉じるように亀裂表面に働いている。この点で、固体の範囲内の応力分布は均一であろうがなかろうが、完全に亀裂が閉じているので、まさに隙間がない場合と同等と考えられる。もはや応力集中が亀裂先端にないので、応力拡大係数はゼロになる。このように、ある場合では、亀裂の存在は負荷応力が亀裂付近で強められる原因になり、またある場合では、表面力の利用はこの増大がゼロになる原因となる。
図2.5.2cに示されるように、ウェルズは中心からの距離bの亀裂面の力FAの働いている長さ2cの対称内部亀裂の亀裂先端Aにおいて応力拡大係数K1を決定した。この状態でのK1の値は以下のようになる
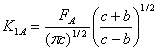
(2.5.2a)
Aにおいて力F Bも、応力場の原因となる。そして、これらの力によって応力拡大係数は以下のようになる
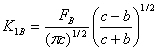
(2.5.2b)
応力拡大係数の付加的性質により、図2.5.2cに示されるように亀裂先端Aにおいて、FAとFBにより総応力拡大係数は以下のようになる。ここでFA=FB=Fである
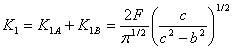
(2.5.2c)
(野澤 訳)
今、もし静止摩擦力Fが割れの長さに沿って連続的ならば、単位長さ当たりの力は割れに垂直なσ(b)に働く応力に関連している。応力拡大係数の総和はdF=σ(b)dbによって代えられたFで、式2.5.2cを積分することで与えられる。
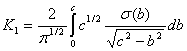
(2.5.2d)
しかしながら、もし力Fが割れを完全に閉じてしまうようなことの表れとして、向きを逆にされたとすると、関連する応力分布σ(b)は割れの始まりよりも前に存在しなければならない。割れを閉じるために働く連続平面静止摩擦について、式2.5.2dによって計算されるような、応力拡大係数は静止摩擦などが不足している場合、巨視的な応力σaを使って割れを計算すると、反対の向きのものを除いて、正確に同じになる。例えば、一様な応力の場合、σ(b)=σaの時に、式2.5.2dは式2.4.1bまで減少する。固体中の亀裂が発生する前の応力場が分かってさえいれば、考えられる亀裂経路についての応力拡大係数は式2.5.2dを使って求められる。ひずみエネルギー開放率Gは式2.4.5bから計算できる。もちろん、固体中の特定の経路に割れが進むかどうかは、いつもすぐに決められるわけではない。Gの最大値を決めるための多くの考えられる経路について、ひずみエネルギー開放率を計算することは必要である。結果として、Gが最大値になる割れの拡大は、実際の割れが進むということである。
(保苅 訳)
脆性材料において、通常であれば亀裂は表面欠陥を基点とする。
亀裂の無い応力領域からの計算による(例えば、先にいくつかの欠陥があった場合の)ひずみエネルギー解法率は続いて起こる亀裂の完全な成長に適合する。
この亀裂成長の測定状態は亀裂の無い応力領域に依存する。
エネルギー解法率Gは、亀裂の無い応力領域に存在する亀裂成長に対する全欠陥を詳細にすることで使われることが出来るが、実際には最初に伸展した亀裂の欠陥にのみ適用できるとされる。
大きな値の亀裂もしくは表面欠陥が存在するとみなした場合を仮定した時、最初の伸展は亀裂の無い応力領域を利用して計算されたGの最大値で与えられた亀裂成長の増分である。
続いて起こる成長の欠陥は、亀裂の無い応力領域を使うまで、亀裂経路に沿って計算された値に適合したグリフィスのエネルギーバランス条件(例、G>=2γ)と関係し、実際の応力領域が亀裂拡大の存在に対し異なっているとしても成立する。
2.5.3 有限要素法を使用した応力拡大係数の測定
応力拡大係数は有限要素法を使用して計算される。
有限要素法は要素で構成されると仮定した固体内における応力状態の測定に便利であり、荷重が応力領域に対して単純な解析解のような場合では不便である。
所定の座標における局所応力と変位に対する有限要素解の構成値は「節点」と呼ばれる。
熟慮の末に選択した座標(r,θ)による局所応力σyyの値は応力拡大係数K1を測定する事で使われることが出来る。
例えば、θ=0の時に式2.4.1aは次の式で与えられる。
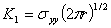
(2.5.3a)
ここでσyyは距離rにおける局所応力値である。
亀裂先端地(r=0)と一致する節店上の応力は、そこの応力特異性により利用できない。
亀裂先端から離れた点・塑性域の外・もしくは正しく「非線形」域で計測された応力拡大係数のみが使用可能である。
しかし、亀裂先端から非常に離れた節点の値には使えず、このことは式2.4.1aはrが微小のときのみ適用できることに由来する。
rが大きい時、式2.4.1aで与えられたσyyが0に接近し、そうでない時、σaとなる。
(塚田 訳)
K1の値は有限要素の結果と式2.5.3aを使うことで決定され、どの節点が用いられても同じになり、以前に述べたrの選択に関連する条件に従う。しかし、用いるrの値とそれに関連するσyyの選択は常に容易ではない。有限要素モデルにおいて、試験片の形状、亀裂先端付近の節点密度、使用した要素の種類は、得られる応力場の精度に影響を及ぼす。K1を推定する最適化の1つの方法は、亀裂先端前方にθ=0の線を取り、その線に沿って異なるrの値を決め、K1を決定するものである。これらのK1の値は滑らかな曲線を描き、r=0におけるK1の値が推定される。その様子を図2.5.3が表している。
3章
遅れ破壊
3.1 はじめに
脆性材料において破壊は大抵、内部亀裂というよりも表面の亀裂の成長によって発生する。環境条件に応じて、脆性固体は時間遅れの破損を示し、最初に荷重が与えられてからある程度の時間が経過した後に破壊が発生する。このタイプの時間遅れ破損は通常、すでに存在している亀裂が成長し、グリフィスのエネルギー平衡方程式における臨界サイズに達することで発生する。臨界未満の亀裂成長は、構造体に使用される脆性材料に作用する安全なレベルの応力の決定において重要である。実際、試験片では耐用年数の決定のために、耐力よりも高い応力を作用させ、設計応力に耐える能力を試験されている。この章では、ガラスの亀裂成長における環境の影響について詳しく学ぶが、その一般的原理は他の脆性材料にも適用できる。ここで話される原理は、脆性亀裂についてのことであり、押し込みの荷重を受ける試験片の耐用年数の決定に特に役立つ。
(Aiman 訳)
3.2 静的疲労
ガラスの強さは極めて変わりやすい。また、経験的にそれが次のものに依存していることが分かっている。
-
荷重率。
荷重が速く、あるいは短い期間で作用する場合、ガラスはより強い。Wiederhornは、1899年にこの性質を観察したGrenetに引き合いに出し、 しかしそれを説明することができなかった。その時以来、他の研究者が同様の結果について説明した。
-
表面の磨耗の程度。 脆性固体の強さに適用されるような多くの破壊力学は、この主題に熱中される。ほとんどの重要な仕事は、 1913年のINGLISおよび1920年のGRIFFITHから始まっている。
-
環境の湿度。 Orowanは、1944年に、雲母の界面エネルギーが(従ってその破壊靱性)、水蒸気の重要な割合を含んでいた空気より真空の方が3. 5倍より大きいということを示した。その時以来、多くの研究者が、負荷応力と併せる水の存在がガラスを著しく弱めることを実証した。
-
温度。 1957年KropschotおよびMikesell、他の研究者達は、ガラスの強さが低温で増加して、時間依存の破壊は極低温度で重要で ないことを 示した。
ほとんどの材の破壊に対する抵抗は、2章に導入されたように「平面ひずみ破壊靱性」K1Cによって便利に表される:K1Cは、アーウィンの応力拡大係数K1の臨界値である。
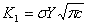
(3.2a)
σが負荷応力、Yは幾何学的形状係数、cは亀裂長である。負荷応力拡大係数はK1< K1Cの関係にあり、亀裂成長は環境の影響に起因していると考えられる。これらの下の条件の亀裂成長は「サブクリティカル亀裂成長」あるいは「静的疲労」と呼ばれ、荷重が最初に作用してから時間経過後、結局破壊へと導く。