英文輪読第1回 4月15日
高橋
TOPへ戻る
'青柳'訳
5.4.2 球状圧子
球状圧子直下の垂直圧力分布は以下の式で与えられる。
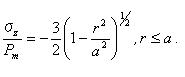
図5.4.1に見られるように、式5.4.2aで与えられる圧力分布に対して、σz=1.5pmは接触円の中心において最大値であり、接触円の端においては0である。接触円の外側では、垂直応力分布は0であり、自由表面である。
接触円内の試料表面上の点の変位は、元の試料の自由表面を考慮して測定され、以下の式で与えられる。
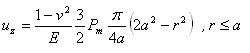
式5.4.2bと5.4.2cは試料表面上の点の変位を表し、この変位は式5.4.2aで与えられる圧力分布に支配される。完全剛体圧子などの特殊な場合に対し、r=0のときの式5.4.2bの値は元の試料表面からの侵入深さと、試料と圧子の2点間の距離を表す。しかしながら、大抵は圧子の弾性変形も考えねばならない（6章参照）。式5.4.2bは接触円の元の表面からの深さを示し（r/a=1において）、正確にはr=0における全深さの1/2である。式5.4.2bと5.4.2cを用いて算出される表面上の点の変位は図5.4.1に示してある。
接触円内では、表面の半径方向の応力分布は
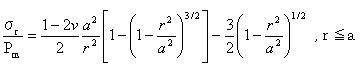
接触円外側の表面では
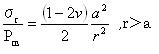
で示される。
TOPへ戻る
'福島'訳
接触円の外側表面における半径方向の転移およびしたがって半径応力はどんな接触円の中の圧力の対称分布でも同じであることを示すことができる。すなわち方程式5.4.2eはｒ＞aであるためには円筒形や円錐の圧子になる。 σｒの最大値はｒ=aで起こる。方程式5.4.2dと5.4.2eを使って計算された材料の表面の半径応力は図5.4.1に示される。半径方向の圧子の真下の表面における点転移は以下によって与えられる。
ここで留意すべきはｒ＞aのすべての値において表面の点転移は接触の中心に向かって内側となる。接触領域の外側で半径方向の転移は前に（方程式5.4.1i）によって与えられた一様圧力のケースと同じであり以下のように与えられる。
表面における円周応力は常に主応力であり接触円の外側は半径応力の大きさと等しい。
試料内部では、応力は以下の式で計算される
ここで、uは以下の式で計算される。
この式はz=0でかつr/a<1の時注意しなければならず、その場合5.4.2式によって与えられるuの値は常に0である。しかし圧子の真下の応力の状態はzの値を十分小さくとることによって適当な精度で計算される。
TOPへ戻る
'坂井'訳
rz面の主応力は次の式で表される。
>
σ1がはたらいている平面の法線とr軸（試料表面 図1.1.10参考）とのなす角は次の式から得られる。
ここで、±はτrzの符号である。たとえ第４象限（z方向が負）を用いた押し込みの応力場を示すことが習慣となっていても、この本に載っている角度を含む全ての式では第一象限がx軸（あるいはr軸）とy軸（あるいはz軸）が共に正である一般座標系をとっている。それ故に、5.4.2o式において、θpの正の値はr軸正方向から反時計方向にσ1の作用線方向にとっている。
表面で(z=0でありr/aのすべての値のとき)、またr=0でz軸に沿った圧子の真下では、σr・σθ・σzは主応力である。円周応力、σθはいつでも釣り合っているから主応力である。試験片の表面では、圧子の真下（ｒ＜a）で、３つのすべての主応力は圧縮で、すべてはほぼ同じ大きさの値である。接触円の外側で、まだ表面上だが、第１の応力σ１＝σrは接触円のエッジ部分で最大の引張りの値を持つ。この応力はヘルツコーン亀裂の形成に関与している。第２の主応力であるσθに等しいσ2は円周応力であり、またこの領域で圧縮である。表面に沿って接触領域の外側では、σ2は−σ1に等しい。またr=0で対称軸に沿った表面の真下では、二つの主応力は等しくσ2はσ1に等しい。表面でのσ3の大きさは接触円の外側ではこの領域において自由表面に対して垂直に働いているから0である。表面に沿ってr/aのすべての値では、σ1はσrに等しく、半径方向に働く。 σ2はもちろん円周応力であり、σ3は表面に垂直に働く。
TOPへ戻る
'伊藤'訳
脆性材料の円錐状の破壊が開始するにあたって重要な押し込みによる応力場の特徴は、ちょうど接触部位の外側にある試料表面の引張領域にあります。
圧子への荷重が十分あるとき、発生する特徴的な円錐の亀裂は、σ１が最も大きくなるところに接触している円上の近くで始まるように見え、そして下外側方へと向かいます。
脆性固体のひびは、引張応力の最大値の直交の方向にたどる傾向があります。つまり、σ１のことです。
したがって、こういった円錐の亀裂を観察することは難しいことではなく、これらが試料の下方へと進むとき、σ１の軌道に直交な応力σ３の軌道をたどるとされます。
しかし、多くの材料において、計算された応力軌道によって書かれた線と実際の亀裂の円錐曲線の一部の間で不一致が出てしまいます。
TOPへ戻る
'広瀬'訳
σ1＞σ2＞σ3のように常に応力を分類するのに便利である。
図5,4,3は式5,4,2iから式5,4,2nまで使用し、算出された等応力曲線を示している。
ただし、図5,4,3の(a)から(e)で示す輪郭はこれらの圧力の方向や作用線を示さないので注意せよ。
それらは単に応力曲線を調べることで得られる。
応力曲線は主応力の接点方向を示す接線であり、特に主応力の方向の可視化に役立つ。
円応力であるσ2の応力曲線はｚ軸周りの円である。
σ1とσ3の応力曲線は式5,4,2oから決められ、図5,4,3(f)と(g)に示されている。
TOPへ戻る
'高橋'訳
計算から、ガラスのポアソン比は０.２１で、円錐のひびの角度はシグマ３の軌道から約３３°の角度で見本の表面にできる。実際の角度はポアソン比に依存する。
しかし、実験の結果では角度は最大１０°減ったときとても浅くなる。
ラウン、ウィルシャウそしてハートレイが解析計算のこの不一致を決議したが失敗した。
ヨフィーは、実際の円錐のひびが固体を通じて進歩するとき先存の応力の範囲が変化すると予測し、そしてラウンは、強い応力をひびの先端にくわえると弾性属性の変化すると提案した。
図5,4,3から見られるように、最大せんだんの起こる位置は、０．５aそして0.49pmについてもっとも重要な深さである。
接触負荷における塑性変形は、通常、これらのせんだん応力の結果延性材料におこる。
TOPへ戻る
TOPへ戻る
英文輪読トップページへ
新田研究室トップページへ
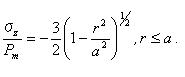
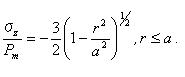
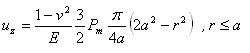
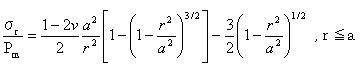
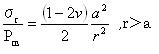