5.4.3 円筒ころの(二次元)接触
前回の節で、平面上の3次元押し込みの場合、半無限半空間における圧力分布と球状圧子に関連付けられて受ける弾性方程式を要約した。この2次元アナログは無限に長い円筒ころに取り付け関連付けられた線である。この場合、圧子荷重Pは試験片の単位厚さ当りの力で与えられる。ジョンソンは接触面積上の圧力分布は以下で示す。
5.4.4 円筒状(平パンチ)圧子
平面の押し込み、円筒平パンチによって生成された応力場は、それを含んでいる古典的なヘルツの応力場に似ている。多くの点で、接触半径は一定であり、圧子荷重は独立していることにより、平パンチの形状は球状が推奨されている。したがって解析する変数の数を減らしている。さらに、複数の円錐亀裂の始まりは、円筒パンチが原因で、接触部が拡大中に球状圧子とともに生じるが、避けられる。しかしながら、円筒パンチ圧子の鋭い端で応力場の特異性を引き起こす。これは試験片または圧子材料の塑性変形を引き起こす。しかしながら、もし圧子の荷重がそれほど大きくなかったら、そのときは接触円の端で起こる小さな塑性変形は試試験片材質の中で弾性圧力分布はほとんど影響しない。
円筒形のパンチ圧子に関連する応力場は、バークインとマーギスによって近年処理され、スネッドンやその他人々によって分析的に決定された。応力場は、圧子の下の圧力の分布に基づいたブーシン応力場の重ね合わせによって計算されている。剛体の円筒形平面パンチの場合、接触圧力分布は次のように与えられます。
図5.4.1(a)を見ると、シグマz=0.5Pmは接触の中央で最小であり、端では無限に近づく。圧子の外側では、表面に沿ってシグマz=0である。圧子の下側では、Uzは元の試料の自由表面下の侵入深さであり、次の式からわかる。
これはrと無関係である。接触円の外側では、垂直変位は次の式から与えられる。
式544bと式544cから計算された表面上の点の変位は図541bに示される。円筒状パンチ圧子についての表面上の応力は次の式から与えられる。
接触円の外側で、円筒パンチ圧子にそって半径方向の引張応力は、式542eから与えれる球状圧子と正確に同じで、半径応力は図541aから示されるように計算される。表面上の半径方向変位は次の式によって与えられる。
式541i、542gと式544fは等しいということに注意しなさい。半径応力と球状と円筒状のパンチ圧子両方の接触円の外側の表面上の変位は、Pmの値と同じに相当する。正数zの方向は負荷投入の方向だということにも注意しなさい。
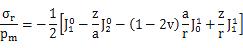
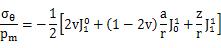
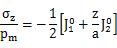
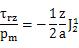
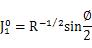
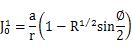
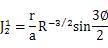
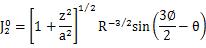
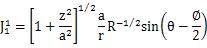
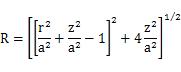
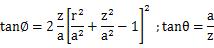
固定された円錐状の圧子によって荷重を受けている半無限の半空間の内部での応力は重要で実際的関心があります。なぜなら、これに近いものが第9章で様々な硬さ試験法を説明するのに使われるからです。ここに示した方法は、前(のページ)で説明した筒状の平パンチ圧子の形式と同様です。接地圧分布は、図.5.4.5(a)で示されており、次の式によって与えられます。
この項目で説明されているすべての場合において、αは円錐の半角で、cotαの大きさは、接触円の半径に対して測定された貫通した深さを表します(図10.4.2参照)。よって方程式で、cotαは次のように平均接地圧の観点からの関数で表されるでしょう。
平均接地圧が円錐の角度だけに依存して荷重Pから独立していることに注意してください。
圧子の下で、元の試験片の表面における変位は以下にように与えられます。
試験片の表面の下の接触の円の深さはr/a=1のときの方程式5.4.5cよって与えられています。
方程式5.4.5cと5.4.5dを使用することで計算された表面における変位は図5.4.1(b)になる。表面の圧力は
また
そして、r
また
σr、σθ、σz、は接触円のすべての点において、主応力である。接触円の外側では、資料表面において、半径方向と円周方向の応力は、以下の方程式5.4.5fと5.4.5.fで与えられるが、それらは円筒形状や球状の圧子の方程式とまったく等しい。
表面における半径方向の応力は方程式5.4.5.を用いて計算でき、図5.4.1に示されている。
r<aにおいての半径方向の変位は以下の式からもとめられる。
そしてr≧aのとき
それは、方程式5.4.5.bを使うことによって、球状や、円筒形状の式(ur)と等しくなり、また均一の圧力の場合である。
試料の内部の幾つかの点では、以下の式で表される。
ここに
第六章 弾性接触
6.1 ヘルツの接触方程式
2つの弾性個体間の接触より発生する応力とひずみは、硬度試験、工業用セラミックの磨耗と衝撃損傷、歯の人口装具の設計、歯車、ボール・ローラーベアリングなどに実際に適用される。多くの場合、剛体圧子と平らで広い試料の間の接触は特に興味深い。もっともよく知られた状況は、ヘルツが接触円半径aは圧子荷重Pに関連があることを発見した、剛体球と平らな表面の接触である。 それによると、圧子半径Rと物体の弾性は以下の式で示される。