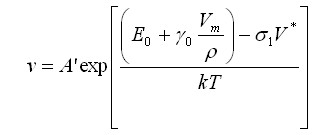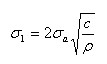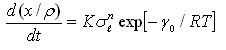1.AZLI  2.渡辺  3.戸松  4.目黒  5.鈴木  6.小野崎

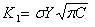
ここで、σは負荷応力、Yは幾何学的形態の要因、そしてCは亀裂長である。　負荷応力の強度要因がK₁ < K_1cとなると、亀裂成長は実験環境の影響によって進行する。　このような状態での亀裂成長は「サブクリティカル亀裂進展」あるいは｢静的疲労」と呼ばれている。　そして結局は最初の荷重が加えられた後しばしば破砕してしまうのである。

　実験で臨海前の亀裂進展以下では検地できないか、まったくおこらないかのどちらかであり、負荷応力拡大係数が物質に依存しK₁=K_1sccであることが示されている。K_1sccはしばしば「静的疲労限界」とよばれる。静的疲労限界付近でのガラスの亀裂成長の実験結果は広く報告されている。ShandとWiederhornとbolzとMichalsskeは、ソーダ石灰ガラスの疲労限界を0.25MPa m^1/2と報告した。wiederhornはK1sccが0.3MPa m^1/2であるとほのめかし、WanとLatherbaiとLawnはソーダ石灰ガラスの静的疲労限界が約0.27MPa m^1/2と報告した。これは一般に受け入れられているが、より実験データによりK₁<K_1sccにおいて完全にとまるかどうか、またはそのような成長が極めて低い確率でこの領域で起こるかどうかを明らかにする必要がある。
上記のことを述べ亀裂長の変化を提案した一方でCharlesとCharlesとHilligは亀裂先端の特性を熱力学や幾何学の観点から亀裂速度について述べた。charlesとHilligは負荷応力や環境によって材料の亀裂先端における分解速度の増加や減少につながるか亀裂先端半径の変化であるかである、それ故に時間とともに変化する（Inglis）応力集中係数に対応する。応力集中係数の変化はある状況下で最終的な結果として局所応力レベルで材料の破損を引き起こす。それらの法則」はある状況下で亀裂先端の鈍化か静的疲労限界をひきおこす。時間変化による亀裂先端の幾何学的変化が原因で亀裂長の変化が原因でないと述べるべきである。CharlesとHilligの応力腐食法則はかなりの歴史的重要性があり、現代の建築学のガラス設計戦略の基本形になっている。この理由でその詳細をここで考える興味を私たちにあたえる。

3.3 チャールズとヒリッグの応力腐食理論。

チャールズとヒリッグは熱力学と幾何学の条件に基づく時間遅れ破壊の理論を開発した。彼らは、水の存在がガラスの化学腐食の原因となるが、それは応力を維持できない反応生成物を生産するからである、と提案した。また、化学ポテンシャルに依存していることに加えて、反応速度もまた局所応力の大きさに依存する。局所応力の大きさは　イングリス応力濃縮係数によって拡大された外部的負荷応力により与えられる。チャールズとヒリッグは、傷の先や亀裂における大きな応力が、それらの場所において優先的に腐食が起こる原因となると推測した(図3.3.1を参照)。これは、亀裂の先の形状を変化させる効果を持ち、またそれゆえに形状の変化による局所応力水準は、応力濃縮係数の大きさを変化させる。

亀裂先端における応力と腐食速度は互いに依存している。チャールズとヒリッグは以下の反応速度式によって、材料と環境の界面の正常な腐食の速度について説明した。

 

 

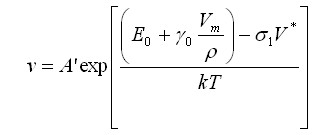
この方程式で、A'は材料の要素の特性、E₀は応力が存在しないとき活性化エネルギー、γ₀は表面フリーエネルギー、V_mは材料のモル体積、ρはひびの湾曲の半径、V^*は活性化体積と定義され、応力に関して活性化エネルギーにおける変化と等しい（dE/ds）、σは反応部位(亀裂先端)の局部応力、kはボルツマンの定数、そしてTは絶対温度である。

方程式3.3aは亀裂速度、または亀裂表面の速度を与えます。(そこでは、反応生成物が少しの圧力も運ぶことができないと思われます)。ひびの先における圧力の大きさはイングリス形状係数(第2章を参照する)から見つけられます。(それは、平均した負荷応力と亀裂先端の形状で表現された局部応力レベルを与えます)。

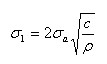
そして、ρが公式3.3bでは、亀裂先端半径であり、半分の長さの亀裂がσaである。外部的に適用されているのは、引張応力であり、σ1は亀裂先端で局部応力です。

亀裂先端半径はこれに垂直な方向における変位に対する亀裂に平行な方向において亀裂表面の二次関数の変位からその形状に関して表すことができます。
チャールズとヒリッグは熱力学的で幾何学的なパラメータに関して、この亀裂先端半径における変化より、
亀裂表面における分析的表現に反応速度過程を関係付けることによって変化率を与える微分方程式で得応力集中係数の時間変化率を表した。
微分方程式で、以下は形成されます:

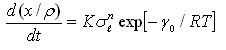
公式３．３cにおいて、Ｋとｎは定数である。ｘは材料の中に亀裂境界の変位を表し、また他の記号は公式３．３aのようにあります。
チャールズとヒリッグは16ものモウルドとサウスウイックの実験結果に合うnの値を指定します。

3.3c式の中のさまざまなパラメータ課題はチャールズとヒリックに３つの可能なレート方程式の解決策を提案するように導いている。そのレート方程式というのは実験的に観測された、腐食と応力の存在による影響を組み合わせたもとでのひびの拡大に関連した事柄を質的に述べている。

1.亀裂は応力集中を高める応力腐食のためにより鋭くなるかもしれない。そしてそれは腐食速度の増加などを導く。 亀裂先端速度はバルクガラスの腐食の割合からわかる。 割れ目は応力集中の増加が材料の理論上の強さと同等の先端応力をもたらす時間tfの後最終的に、起こる。

2.亀裂先端はひびの半径の増加が亀裂の長さの増加のバランスをとっていて丸くなるかもしれない。応力集中係数の増加や、局部応力レベルの増加がなしで。 これらの条件で亀裂の長さが非常にゆっくり増加する。これは事実上、そのひびは負荷応力を無期限に支持できることを意味する。

3.亀裂先端半径、亀裂幅、そして長さは腐食のためすべて増加するかもしれない。有効な応力集中係数の減少、局部応力レベルや溶解速度の減少を通じてこれらの条件で試料はさらに強くなる。