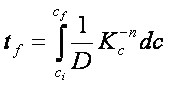英文輪読第2回 4月30日
TOPへ戻る
渡辺 訳
3.3C式の積分は負荷応力、温度、そして表面形状の欠陥を与えることによって破壊時間を計算することができる。
チャールズとヒリングは、亀裂長の変化率よりもむしろ亀裂先端の範囲の変化率の方が応力集中の変化において最も信頼できる要素である、ということを主張した。
積分を簡略化するために彼らは、亀裂長は基本的に限られた範囲以上の応力では一定である、ということを仮定した。
これは積分は亀裂長の微小変化を負荷応力によって生じた先端部の大きな変化として扱うように解釈される、という意味を含んでいる。
これは負荷応力が疲労限度と関係がある要素よりも小さい場合のみに使われる。
そして疲労限度において、応力水準の微小変化は、それとは桁違いの亀裂速度の変化によって生じる。
3.3b式と3.3c式の合成によってブラウンは、先ほどの仮定における失敗を引き起こす決定的な間違いと以下に示す合成式を証明することができた。
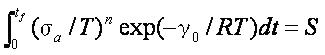
ここで、Sは一定値である。
この重要な合成式は最新の窓ガラスの破壊予測モデルの基礎となっている。
(例えば、ガラスの破壊予測モデルや負荷持続理論などに用いられている。)
戸松 訳 訳
チャールズとヒリックの法則によると上記の項目(ⅱ)が先端応力が根本的な物質の引張応力には達しないという状況から確認された”疲労限界”の存在をほのめかした。
チャールズとヒリックはモールドとサウスウィックのガラスの疲労強度におけるかれらの実験データの申請が疲労限界における負荷応力がσaで液体窒素の温度における破壊強度がσnで0.15で疲労効果は証拠がないことを導いた。
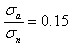
K1sccが疲労限界を表したアーウィン応力係数に関して表現すると、これがガラスになる。
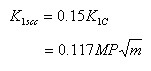
鈴木 訳 訳
ワイダーホーンは1977年にK1が0.3MPam1/2以下で亀裂速度が急に低下することを示し,それはチャールズとヒリッグによって予測された値よりいくらか大きい値である。
疲労限度の存在はチャールズとヒリッグの研究で絶対的であるがマーシュによって注意が投げかけられた。
彼は亀裂先端での塑性流動に関してガラスの静的疲労と破壊を述べた。
マーシュは理論上の引っ張り強さ以下での応力でのガラスの塑性流動の実験から根拠を示した。
流動応力は温度や時間に依存する。
塑性流動は大きい応力が加えられた亀裂先端に生じ、これはアーウィンの理論からである。
この領域は”亀裂先端塑性領域”と呼ばれ、その大きさは以下の式で算出される。
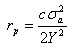
ここで、rpは塑性領域の半径である。
cは亀裂長さ。
σaは負荷応力である。
また、Yは材料の降伏力である。
破壊は塑性領域が臨界サイズに到達したとき発生する。
その流動応力σyは、しかしながら、時間と温度に依存する。
それは破壊応力σaに違った周囲の状態から得られることを許す。
この研究は破壊応力において時間や温度の変化による影響を含めることを除いてアーウィンが考えた概念であるK1cの別の可能性を見出した。
小野崎 訳 訳
特に興味深いのは、静的疲労限界に関する亀裂先端塑性の影響である。MarshはCharlesとHilligの理論(これは脆性破壊理論に基づく、すなわちGriffithのエネルギーバランスとInglisの応力集中係数)は低疲労限界におけるShandの実験的なデータに適用する際に3Åの亀裂先端速度を必要することを提示した。Marshは高められた応力による腐食の自然選択はそのような小さな半径をもたらさないだろうと主張した。実験的な証拠は塑性領域は20Åのオーダーであるべきで、Marshの計算はガラスの60Åの値を示すことを意味する。Marshはわかった。性的疲労限界におけるガラスの強さは塑性領域の大きさに関して、CharlesやHilligの速度方程式よりむし
ろ正確に表していたことが。かれは主張した。分析が説明する。すべての機械の脆性破壊理論に基づくガラスの性質やそれらに基づかない付加的な問題を。
一般的にCharlesとHilligの応力腐食理論は静的疲労の現象を十分に説明するのには不十分だと承認された。しかし物理学の現象に関して説明するよう試みた。
目黒 訳 訳
3.4 鋭い亀裂先端の成長モデル
チャールズとヒリッグの理論は表現しようと試みる、臨界前の亀裂成長の物理学的機構を。
対照的に、多くの研究者は説明しようとしない。鋭い亀裂先端を仮定すること、経験的な数学モデルを使って臨界前の亀裂の速度を説明すること以外に。
図3.4.1のRegion1の亀裂速度は互いに依存していると考えられる。適用された応力拡大係数と、環境における部分的な水蒸気の圧力に。
静的な負荷応力シグマAに関しては、亀裂速度は以下によって与えられる。
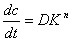
数式3.4aに関して、dc/dtは亀裂速度であり、Dとnは、図3.4.1の範囲Iにおける臨界前の亀裂の成長を特徴付ける定数である。
破壊する時間Tfは、方程式3.4aを統合することによって、見つけられるだろう。
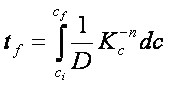
CiとCfはそれぞれ初期的、そして、最終的なひびの長さであり、Kcは値である。K1cの値以下であるK1の。
Tfは時間である。CiからCfまで成長する時の。
TOPへ戻る
AZLI 訳 訳
TOPへ戻る
1.渡辺 2.戸松 3.鈴木 4.小野崎 5.目黒 6.AZLI
TOPへ戻る
英文輪読トップページへ
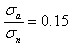
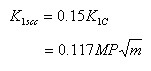
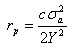
![]()