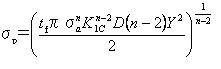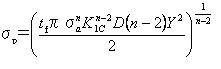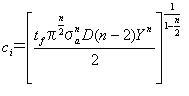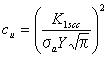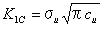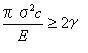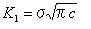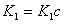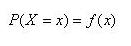英文輪読第3回 5月14日
TOPへ戻る
小野崎 訳
実験結果を使ったlogtfとlogσaのプロットの傾きはnの値によって上がり、式3.4hに置き換えられ、Dの決定を許す。
水に沈められたガラスでは、Weiderhornのデータによると、nは17でlogDは-102.6の値をとるだろうと示されている。
他のnの値は実験的に決定され、表3.4.1に要約されている。
文書からは直接使えるnの値はないが、nの値や式3.1.2を利用して、実験結果のデータのグラフから単純に座標をよんで得る。
前に述べた分析は一般的に鋭い亀裂先端の成長モデルと言われていて、CharlesとHilligの応力腐食理論とは対照的に限界応力のもとでの亀裂の成長を述べている。
3.5 鋭い亀裂先端の成長モデルの利用
鋭い亀裂先端の成長モデルはある試料が、設計応力のもとで意図された寿命まで耐えられるかどうか、決定するための便利な方法を提供する。
たとえば、メーカーはすべての試料が荷重を与えられたもとで、特定の寿命を耐えることを保障したがっているかもしれない。
これをするために、試料は耐力にさらされるかもしれない。それによってそれらすべての試料は、意図する寿命が続かなくなり、サービスに入る前に、機能しなくなることを引き起こすだろう。
鈴木 訳
図3.5.1に示されているグラフを考えてみよう。
一様な負荷応力σaで試料の寿命tfの間、ciよりも大きな亀裂の長さは臨界サイズになり、試料の破壊を招く可能性がある。
したがって、ciよりも大きな亀裂がある試料をひとまとめに取り除くことが望ましい。
残りの試料はciよりも小さな亀裂の大きさを持っているだろうし、それらの亀裂はtfという時間の間サブクリティカル亀裂進展を受けるだろう。
しかし、その時間の間には臨界サイズacには届かないだろう。
ciよりも大きな亀裂を保有している試料は亀裂の大きさに対してすべての試料を臨界サイズまでもっていくことで、その処置を行う前にすぐに破壊する。
それらciより小さな亀裂を持っている試料は破壊しないだろう。
それら残りの破壊されていない試料は時間tfの間に負荷応力によって破壊しないと思える。
試料が保有している亀裂はその時間の間確かに広がっているがσaのために臨界サイズまでは広がらない。
適用する耐力σpは公式3.4fの展開から求めることが出来ます。
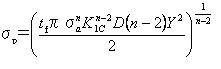
亀裂の大きさciは以下から求められます。
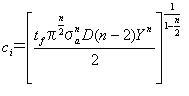
渡辺 訳
しかし、これは静的疲労限度K
1SCCの存在を示す有力な証拠がある、という風に理解されるかもしれない。
その証拠とは、応力拡大係数が小さい場合サブクリィティカル亀裂進展が発生しない、というものである。
欠陥寸法c
iが静的疲労限度に対応するような別の欠陥寸法よりも小さいかどうか、ということはσ
aの値によって決めることが可能である。
よって、K
1SCCは材料特性となるので、負荷応力σ
aによる臨界欠陥寸法は次の式から容易に理解することができる。
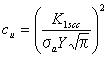
ここで、もしたまたまc
uが既値の値σ
aに関するc
iよりも大きい場合、c
uよりも大きい欠陥のみt
f秒の間、サブクリィティカル亀裂進展が発生することになる。
このような場合、必要な耐力は図3.5.1に示されるような3.5a式によって求められる値よりも小さい。
欠陥寸法に関する臨界応力c
uは次の式から確認することができる。
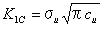
ここで、σ
pとσ
uどちらを耐力とするべきであろうか?
1,3.5c式を用いてc
uの値を計算する。
2,3.5b式を用いてc
iの値を計算する。
3,もしもc
iがc
uよりも大きければ、必要とされる耐力はσ
pである。(3.5a式より)もしもc
iがc
uよりも小さければ必要とされる耐力はσ
uである。(3.5d式より)
戸松 訳
耐力の適用は臨界サイズでの破損によるキズを含む試料の破損を保障する。
そのような長さのキズは前から存在するが過重下での臨界前の亀裂進展の結果であるかもしれない。
しかいもし臨海前の亀裂進展が過重下ではないときに起きたら耐力試験の結果そのときの試料が臨界サイズよりもキズの長さが大きいものを含むかもしれない。
そのような潜在的に危険なキズなのでその耐力試験の方法では発見されないだろう。
この可能性を最小限に抑えるために過重のない順序はできるだけ早く実行されるべきである。
第4章 脆性破壊の統計値
4.1 序論
脆性固体の破壊はグリフィスの亀裂成長の基準によれば引張応力場の存在下で普通表面のキズや亀裂の存在が原因でおこる。
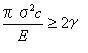
式4.1aの一方では歪みエネルギーバランス基準はアーウィンの応力拡大係数に関して示されることもできる。
目黒 訳
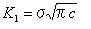
ここで、σは負荷応力であり、cは亀裂の長さである。
幾何学的な形状係数Yは、時々この定義に含まれるが、ここには示されていない。
K1の臨界値(K1Cと呼ばれる)は、材料の破壊靭性である。
一価の具体的な特性が、ほとんどの材料にあるとK1Cは見なすことができる。
以下の時に,
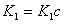
亀裂は広がっていき、ことによると見本の破壊につながるだろう。
ワイブル統計は見本の破壊の原因となりうる傷の存在を予測するために使用される。
必ずしも材料力学に関連していないさまざまな状況で役に立つことをワイブル統計は証明した。
脆性固体の破壊に適用されたとき、ワイブル統計は、特別な負荷応力で瞬時に起こっている破壊についてあてはまる。
しかしながら、臨界未満の亀裂の成長という現象は含むことができる、引張応力がかけられた見本の耐用年数を予測する目的を。
4.2 基礎統計学
Xは、いくつかの出来事に関連している何らかの確率変数であるとする。
例えばXは、2回のコイントスのときに得られた頭数であるかもしれない。
Xの各値には、発生する確かな確率があり、以下で与えられる。
数式3.4aに関して、dc/dtは亀裂速度であり、Dとnは、図3.4.1の範囲Iにおける臨界前の亀裂の成長を特徴付ける定数である。
破壊する時間T
fは、方程式3.4aを統合することによって、見つけられるだろう。
C
iとC
fはそれぞれ初期的、そして、最終的なひびの長さであり、Kcは値である。K
1cの値以下であるK
1の。
T
fは時間である。C
iからC
fまで成長する時の。
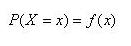
TOPへ戻る
AZLI 訳
TOPへ戻る
1.小野崎 2.鈴木 3.渡辺 4.戸松 5.目黒 6.AZLI
TOPへ戻る
英文輪読トップページへ