第4回英文輪読5月21日

英文輪読第4回　5月21日

鈴木　訳

図4.2.3に示されているように確立を与える関数ｆ(x)の曲線下の範囲であることを意味する。連続的な場合に関して、いくつかの地点では関数f(x)の値は確立ではない。正確に言えば、関数f(x)は確立密度関数と呼ばれている。累積分布、関数f(x)は連続的な場合に関してx以下のある値Xをとる確立を与え、以下から導くことが出来る。

siki

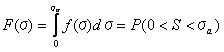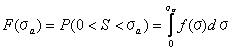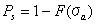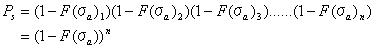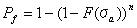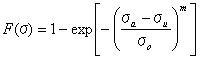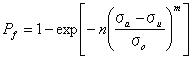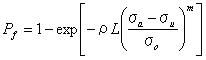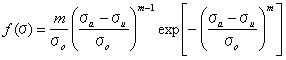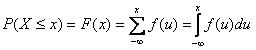
関数f(x)の値は図4.2.3bに示されているようにxが増加するにしたがって1に近づく。方程式4.2dと4,2eは確立の基礎ルールを満たしている。

4.3　ワイブル統計

4.3.1　強度と破壊確立
図4.3.1に示されているように、負荷Wがつるされているn個の連結からなる鎖を考えてみよう。負荷によって、応力σ_aは鎖のそれぞれの連結部分において引き起こされる。しかし、現在の研究では私たちは連結部分が引っ張り状態でただ破壊し、Sは0よりも大きいと仮定する。もしくはもっと現実的に、Sはσ_uより大きく、そこでのσuは0以上であり引っ張り強さの低い限界値である。すべての連結部分はσ_u以上の引っ張り強さを持っていると言われている。

TOPへ戻る

戸松　訳

（今のケースで）連続確率変数を含む分布に関して、ひとつの連結部の持つ特定の値σ_a以下の引張り応力ｓの定義は一般に確率密度関数ｆ(σ)の積分により与えられる。

f(σ)は累積する確率関数をあらわす。そして確率密度関数f(σ)はより下の蓄積された領域をあらわす。ｆ(σ)は増加するσ_aとともに増加する。ｓ＞０なので、f(σ)が０→＋無限の合計での領域は１に等しい。 σaが負荷応力ならば何が鎖の破損の確率はいくらか？その鎖はｎ個の連結部をもたせる。

siki

今、その鎖が負荷応力σ_aで破損するだろう。ｎ個の連結部のひとつが強度ｓ≧σ_aをもつとき連結部の増加は鎖に弱い連結部が存在する可能性が高いことにつうじる。だから、私たちはｐ_ｆがｎとともに増加することを期待する。 f(σ_a)はｓ<σ_aで連結部のある可能性を与える。ｓ＞σ_aで連結部の可能性は

siki

なぜならばf(σ_a)の０→∞の積分が１になるからである。

TOPへ戻る

小野崎　訳

したがって、n個の連結部すべてがσ_aより大きなSを持つ可能性は個々の可能性の生成によって決まる。

siki

ここでP_sは応力σ_aの荷重を与えられたときのチェーンが生き残る可能性でF(σ_a)はそれぞれの連結部で同じである。式4.3.1dはすべての連結部が同時に破損しない可能性を与える。チェーンが破損する可能性はしたがって、書き留めることがとても重要。

siki

わたしたちはチェーンの破損の可能性と同時に存在する、すべての連結部が破損しない可能性に関して述べなければいけないことを。この理由はチェーンはどれかひとつの連結部の強さSがσ_a以下だと、むしろすべての連結部のSがσ_a以下になり、破損するためである。式4.3.1dによって与えられた可能性はn個すべての連結部に適用する。 F(σ)は何か？ワイブルは単純で便利なもの以外の特定の理由がないとして、蓄積された作用の可能性を提案した。

siki

ここでσ_u・σ_oそしてmは調節できるパラメータで、σ_uは破損が起こらないまでの応力レベルを表す。見てわかるように、σ_oは強さの値の基準の表示で、mは強さの広がりを表現する。

TOPへ戻る

渡辺　訳

4.3.1f式を4.3.1e式に代入したものはn個の連結部を持った鎖が破綻する確率を容易に示すことが出来、その代入式は次のようになる。

siki

ここで、もしも輪の数をあらかじめ知っているのなら、代入式は明確である。しかし、この式は常に成り立つとは限らない。特に、非常に多くの数の連結部を扱っているときは。もしもρが個数あるいは連結部一点あたりの強さだとすると、n=ρLとなる。輪の破綻する確率P_fはこのとき以下の式で計算される。

siki

ここで、Lは鎖全体の長さ、ρは連結部一点あたりの強さの数値である。ワイブルの式における指数はしばしば危険関数と呼ばれ、Bという記号で表される。

4.3.2 ワイブルパラメータ
変数σ_uはそれぞれの連結部の引張り強さの下限値を表す。そして、ここではすべての連結部はσ_uよりも大きな引張り強さを持っている。ここで、負荷応力σ_aがσ_uよりも小さいなら、破綻せずにそのままである確率は１である。変数ｍは一般的にワイブル係数として知られている。そしてそれは統計的基礎の処理を規定する指数である。高い数値のｍは強度のばらつきの範囲が狭いということを示している。（図4.3.2参照）ｍが無限へと近づいていくとき、強度のばらつきの範囲は０に近づく。そして全ての連結部は同じ強度をもつようになる。

TOPへ戻る

目黒　訳

物理的な意味をパラメタσ₀に与えるのは、より難しい。様々な人が、さまざまな説明をするが、多くは定義しようとはしない。ワイブルの公式では、σ₀は単位堆積あたりの応力であり、S=0.63 という破裂の確率を与える。デイビッジは与えた、σ₀は物理的重要性のない、統一されたパラメータである。マテウソンはσ₀は強さの規模を与えると言う。そして、アトキンスとマイは物理的重要性のない、統一されたパラメータであると言う。 σ0は、確かに、強度を分布させる、引っ張り強度に。この理由で、普通は参照の強さと呼ばれる。しかしながら、私たちが見るように、それは与えない、確かな引っ張り強度の繋がりの最大数の場所を。おそらく最初に予想されるであろう方法で。累積確率機能(Fσ)は、式4.3.1fによって与えられる。それは、容易に示すことができる。対応する確率密度関数(fσ)の積分が、式4.3.1aにおいてN=1の場合に。

siki