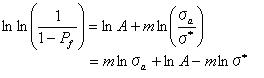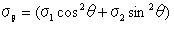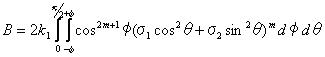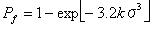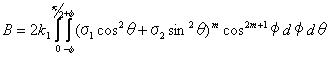4.4 脆性固体の強さ
4.4.1 ワイブル確率関数
領域Aは多くの面積要素daから成り、領域Aの脆性固体を考える。 面積要素は以前に議論した、チェーンのつながり類似している。
1. 各要素daには、関連引張り強度がある。
2. 適用された引張応力の結果、標本の破砕は起こる。どんな面積要素も破壊するとき。
3. 要素は破壊する。含むとき。優勢の負荷応力の大きさによって決まる臨界サイズよりも傷が大きくなることを。
応力σAの要素の破壊の確率は、要素が臨界の傷のサイズよりも大きい、または同じ大きさの傷を含む確率に関連される。
渡辺 訳
一般的に、これらは固体表面の大きさ、密度、そして方向により欠陥分布が存在する可能性がある。
もしも負荷応力によってできた垂直ではない亀裂が同じ大きさの垂直応力によって発生するならば、方向分布はサイズ分布に関連しているだろう。
さらに、破砕を引き起こすような各々の欠陥は「ペニーシェイプトゥ」と呼ばれる欠陥寸法や「スタンダード」と呼ばれる幾何学的破壊解析と同等なものである、と仮定されるだろう。
ρを特定の荷重条件で破綻を引き起こす可能性のある欠陥密度(単位面積あたりの数値)とすると、その場合面積Aでの破綻を引き起こす可能性のある欠陥の合計数はρAである。
後に項ρ(通常はこの数値はわからない)は実験結果から結合パラメータを決定することが出来る項ρ0(これも通常はわからない)に都合よく組み込むことが出来る、という風に解釈されるようになった。
ワイブル確率関数は次のように表現できる。
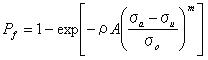
一般的に、応力はある面積Aを超えて一定値になることはない。よってもしσaが位置関数ならば、以下の積分は適切な形となる。
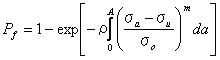
ワイブル自身は関数F(σ)の形に理論的な根拠はないと認めた。しかし、それにもかかわらずF(σ)は多くの現実的な状況で満足のいく計算結果を求めるのに役立つ。 故にF(σ)は実験値からの適切な近似によって得られる3つの変数m,σu,σ0を含んでいる。
鈴木 訳
欠陥密度時間ρをF(σ)の作用下で組み込むことは普通であるから、一様な応力のためにこの場合は以下のようになる。
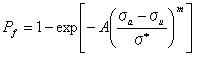
そこでは
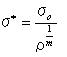
ρとσ0は互いに依存していることは明らかである。 それはρとσ0を単一のパラメーターσ*に合成できるからである。 通常、σ*の値は適当な破壊実験からのみ定めることが可能である。 等化なものを定めることはとても難しい。 ペニーの形、非常に鋭い、試験片のすべての表面の傷による垂直に配向した傷の大きさ。 σ*は表面の性質であり、それはときどき表現するのに実用的である。
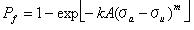
そこでは
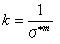
それは、σu=0のとき以下のようになる。
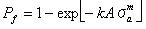
この最近の表現は一般的にワイブル確立関数に使われる。 また、表面の傷の分布特性を伴う範囲Aにおける破壊確率に関係する。 一様な引張応力σaによるmとkによって。
4.4.2 ワイブルパラメータの決定
実際のところ、ワイブルパラメータは実験結果の適切な分析からわかる。 4.4.1cを再配列することで以下のことが与えられる。
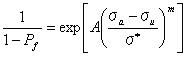
また両辺の対数を2回とることによって以下の式が得られる。
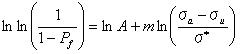
σ0=0とすることによって。(それはすべての応力レベルにおいて0を含め、破壊の確立が存在するということを言っているに等しい。)そして。
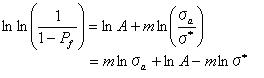
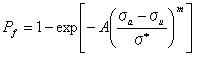
そこでは
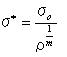
ρとσ0は互いに依存していることは明らかである。 それはρとσ0を単一のパラメーターσ*に合成できるからである。 通常、σ*の値は適当な破壊実験からのみ定めることが可能である。 等化なものを定めることはとても難しい。 ペニーの形、非常に鋭い、試験片のすべての表面の傷による垂直に配向した傷の大きさ。 σ*は表面の性質であり、それはときどき表現するのに実用的である。
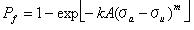
そこでは
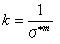
それは、σu=0のとき以下のようになる。
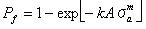
この最近の表現は一般的にワイブル確立関数に使われる。 また、表面の傷の分布特性を伴う範囲Aにおける破壊確率に関係する。 一様な引張応力σaによるmとkによって。
4.4.2 ワイブルパラメータの決定
実際のところ、ワイブルパラメータは実験結果の適切な分析からわかる。 4.4.1cを再配列することで以下のことが与えられる。
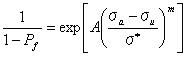
また両辺の対数を2回とることによって以下の式が得られる。
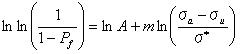
σ0=0とすることによって。(それはすべての応力レベルにおいて0を含め、破壊の確立が存在するということを言っているに等しい。)そして。