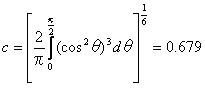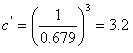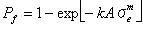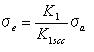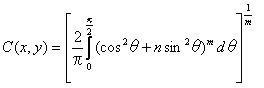
偦偙偱偼値偼嵟戝庡墳椡偵懳偟偰偺嵟彫庡墳椡偺斾棪偱偁傞丅 傕偟憃曽偺庡墳椡偑堷挘墳椡偱偁傞側傜偽丄愊暘偺忋尷抣偼 兾/2 偱偁傞丅 傕偟堦曽偑埑弅墳椡偱偁傞側傜偽丄忋尷抣偼埲壓偺傛偆偵梌偊傜傟傞丅
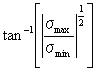
梫慺C(x,y)偼値偑憹壛偡傞偵偮傟偰尭彮偡傞丅 價乕僜儞偲儌儖僈儞偼m偲n偺斖埻偵懳偟偰偺C(x,y)偺抣偺昞傪梌偊傞丅 傂偲偮偼昞4.4.2偵暋幨偡傞丅 嫽枴怺偄偙偲偵丄偦傟偼價乕僜儞偺曗惓棪偑n亖0偱C亖1偱偁傞傛偆偵應掕偝傟偨偐偳偆偐傪帵偟偰偄傞丅 偦傟偐傜n亖1偱們偺抣偼儚僀僽儖偵傛偭偰嶼弌偝傟偨抣偵旕忢偵嬤偄丅 偨偲偊偽丄價乕僜儞偼m亖3丄n亖0偱偦傟傪帵偟偰偄傞丅