1.鈴木  2.目黒  3.戸松  4.小野崎  5.渡辺  6.AZLI

σ_ｒは主応力である。 正接のσ_θとせん断応力τ_ｒθは試験片内のいくつかの地点で0である。 X軸を中心とし、荷重のかかっている地点において接線の直径ｄの円周によってrがdcosθに等しいことを示すことは簡単である。 また方程式5.3.1aによって与えられたσ_ｒは応力特異性が生じるr＝0の地点を除けば円周上のすべての地点で同一である。 (無限の応力と無限の転移) 応力特異性は試験片材料の塑性降伏によって実際のところ避けられる。 それは有限の領域において、くぼみ上の荷重を広げる働きをする。 デカルト座標ではxy平面の応力は以下のとおりである。



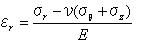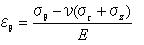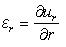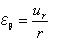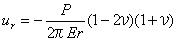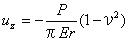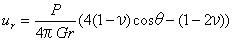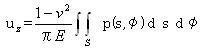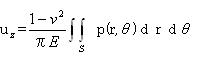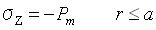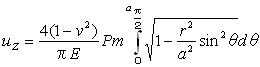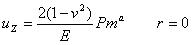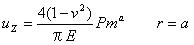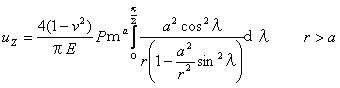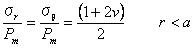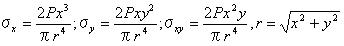
5.3.2　点接触 点接触によって負荷された固体内の応力は原点を除いてブッシーネスクによって算出され、円筒形状の極座標でティモシェンコとグッディアーによって与えられた。









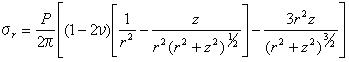
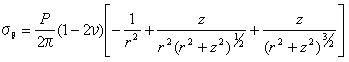
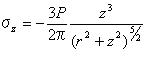
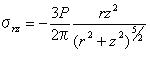
応力σ_z、τ_yz、τ_zxの表面は0である。 方程式5.3.2aを使うことで算出された応力は図5.3.2に示されている。 方程式5.3.2aでそれを注意し、また後節で示される他の方程式にも注意しよう。 座標rとzは多くの論文では垂直下向きとしてzの値が増加するのが普通であるけれども正数として扱われている。 また、荷重Pは下向きに伸びるように示されており正数である。

点dPによってG点における表面のたわみは方程式5.3.2dの変数rをsに置き換えたうzによって与えられる。 点Gにおける表面たわみの合計は各dPにより起こるたわみの合計である。 表面たわみの合計の式uz=f(r，θ)は局所座標やｒやθに関するφにより得られる。 従って、ｒやθに関して方程式5.3.2dに代入すると接地面の部分sを与える。



もしくは



ここで留意すべきは局所座標sとφは考慮中である点Gが対称軸r=0にあるときｒ，θに一致する。 ひずみは方程式5.2.3cとフックの法則からの方程式5.2.3bによって計算されるであろう。 この手順を用いて、たとえば方程式5.2aで与えられた形の圧力分布を示すことができる球状圧子の形で対応する接触円の真下に転移を起こすのを示すことができる。 与えられた圧力分布接地により材料内部の応力の方程式は式5.3.2aによって与えられるブッシーネスク場の重ねあわせから公式化されるだろう。 あるいはまた圧子のため接触円の真下に表面の転移を定め、応力を決めるための積分法を使うかもしれない。