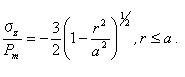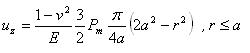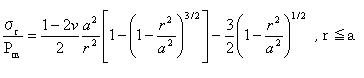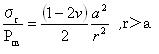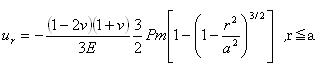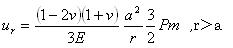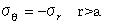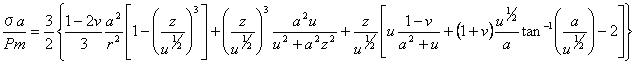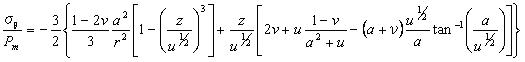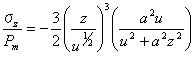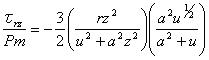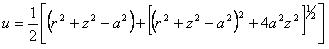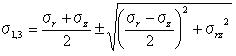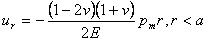
また、
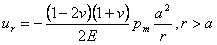
そしてそれは、今の事においてr>aとなるUrは、後の式5.4.2g, 5.4.4f,そして5.4.5jに与えられる、球状、筒状、円錐状の圧子と同じである事を通知するだろう。 試験片内の点において、r=0のZ軸に沿っていて、はチモシェンコとグーディアは与えた。
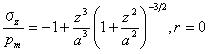
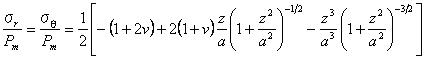
試験片内の点において、スネッドンは与えた。
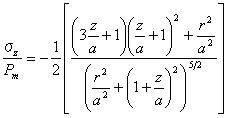
試験片の半分の内部の一般的な点における応力分布の分析的な表現は、式5.4.1bの積分は曖昧な積分で、すべてを解くことはできないが、例として、Z=0、R=0のようにもっとも便利な座標系なので、得ることは難しい。 分析結果の複雑さは、有限要素法を使うことによって便利に迂回することができ、また、内部に含まれる応力分布の、この手順を使った計算は、Fig.5.4.2に示されている。
5.4.2 球状圧子
垂直加重分布の直下の球状圧子は、ヘルツによって与えられた。